
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.
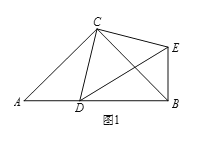
填空: ①![]() 的值为 ;②∠DBE的度数为 .
的值为 ;②∠DBE的度数为 .
(2)类比探究
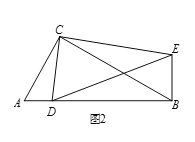
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由.
的值及∠DBE的度数,并说明理由.
(3)拓展延伸
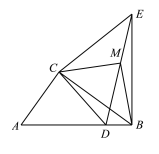
如面3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.

【答案】(1)1,90°;(2)![]() ,90°,理由见解析;(3)3+
,90°,理由见解析;(3)3+![]() 或3-
或3-![]()
【解析】
(1)易得△ABC和△CDE为等腰直角三角形,所以AC=BC,CD=CE,通过证明△ACD≌△BCE,可得AD=BE和∠CAD=∠CBE=45°,进而得出答案;
(2)通过证明△ACD∽△BCE,可得![]() 的值,∠CBE=∠CAD=60°,即可求∠DBE的度数;
的值,∠CBE=∠CAD=60°,即可求∠DBE的度数;
(3)分点D在线段AB上和BA延长线上两种情况讨论,由直角三角形的性质可证CM=BM=![]() ,即可求DE=
,即可求DE=![]() ,由相似三角形的性质可得∠ABE=90°,BE=
,由相似三角形的性质可得∠ABE=90°,BE=![]() AD,由勾股定理可求BE的长.
AD,由勾股定理可求BE的长.
解:(1)∵∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,
∴∠ABC=∠CAB=45°,∠CDE=∠CED=45°
∴AC=BC,CD=CE
∵∠ACD+∠BCD=∠BCE+∠BCD=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE=45°
∴![]() =1,∠DBE=∠ABC+∠CBE=90°
=1,∠DBE=∠ABC+∠CBE=90°
故答案为:1,90°;
(2)![]() =
=![]() ,∠DBE=90°,理由如下:
,∠DBE=90°,理由如下:
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,
∴∠ACD=∠BCE,∠CED=∠ABC=30°,
∴tan∠ABC=tan30°=![]() =
=![]() .
.
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,
∴Rt△ACB∽Rt△DCE,
∴![]() =
=![]() ,且∠ACD=∠BCE,
,且∠ACD=∠BCE,
∴△ACD∽△BCE,
∴![]() =
=![]() =
=![]() ,∠CBE=∠CAD=60°,
,∠CBE=∠CAD=60°,
∴∠DBE=∠ABC+∠CBE=90°;
(3)若点D在线段AB上,如图,
由(2)知:![]() =
=![]() =
=![]() ,∠ABE=90°,
,∠ABE=90°,
∴BE=![]() AD,
AD,
∵AC=2,∠ACB=90°,∠CAB=60°,
∴AB=4,BC=2![]() .
.
∵∠ECD=∠ABE=90°,且点M是DE中点,
∴CM=BM=![]() DE,
DE,
且△CBM是直角三角形,
∴CM2+BM2=BC2=(2![]() )2,
)2,
∴BM=CM=![]() ,
,
∴DE=2![]() ,
,
∵DB2+BE2=DE2,
∴(4-AD)2+(![]() AD)2=24,
AD)2=24,
∴AD=![]() +1,
+1,
∴BE=![]() AD=3+
AD=3+![]() ;
;
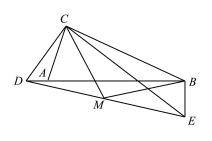
若点D在线段BA延长线上,如图,
同理可得:DE=2![]() ,BE=
,BE=![]() AD,
AD,
∵BD2+BE2=DE2,
∴(4+AD)2+(![]() AD)2=24,
AD)2=24,
∴AD=![]() -1,
-1,
∴BE=![]() AD=3-
AD=3-![]() .
.
综上所述:BE的长为3+![]() 或3-
或3-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P.
(1)求证:PC=PE;
(2)求证:PC是⊙O的切线;
(3)若AB=10,AD=2,AE=![]() ,求PC的长.
,求PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.
(1)求每次降价的百分率.
(2)若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2;以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3;以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长___________.
的长___________.
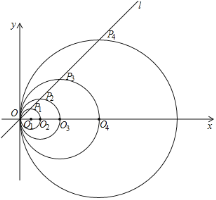
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解停课不停学,期间,同学们居家学习的情况,某校从全校学生中随机抽取部分学生进行网络问卷调查,并将调查结果分成(![]() :优,
:优,![]() :良,
:良,![]() :中,
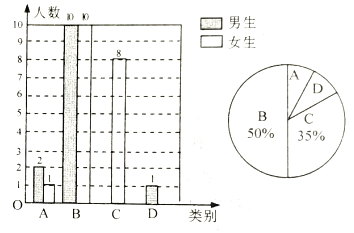
:中,![]() :差)四类.依据调查结果绘制成两幅不完整的统计图
:差)四类.依据调查结果绘制成两幅不完整的统计图
(1)这次被调查的学生一共有 人,其中![]() (中)等次的男生有 人,表示
(中)等次的男生有 人,表示![]() (差)等次的扇形所对的圆心角的度数为 度;
(差)等次的扇形所对的圆心角的度数为 度;
(2)若该校约有![]() 名学生,估计全校居家学习处于优或良(
名学生,估计全校居家学习处于优或良(![]() 或
或![]() )等次的学生有多少人?
)等次的学生有多少人?
(3)为了共同进步,刘老师想从被调查的![]() 类和
类和![]() 类学生中分别选取一位同学进行“一对—”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位男同学的概率.
类学生中分别选取一位同学进行“一对—”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
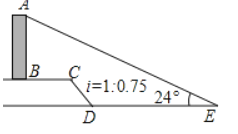
【题目】如图,![]() 是一垂直于水平面的建筑物,某同学从建筑物底端
是一垂直于水平面的建筑物,某同学从建筑物底端![]() 出发,先沿水平方向向右行走
出发,先沿水平方向向右行走![]() 米到达点
米到达点![]() 再经过段坡度(或坡比)为
再经过段坡度(或坡比)为![]() 坡长为
坡长为![]() 米的斜坡
米的斜坡![]() 到达点
到达点![]() 然后再沿水平方向向右行走
然后再沿水平方向向右行走![]() 米到达点
米到达点![]() 均在同一平面内).在
均在同一平面内).在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() 求建筑物
求建筑物![]() 的高度. (参考数据:
的高度. (参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
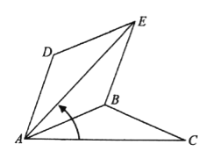
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连结
,连结![]() .
.
(1)求证:![]() ;
;
(2)四边形![]() 是什么形状的四边形?并说明理由;
是什么形状的四边形?并说明理由;
(3)直接写出:当![]() 分别是多少度时,①
分别是多少度时,①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com