
【题目】为了了解停课不停学,期间,同学们居家学习的情况,某校从全校学生中随机抽取部分学生进行网络问卷调查,并将调查结果分成(![]() :优,
:优,![]() :良,
:良,![]() :中,
:中,![]() :差)四类.依据调查结果绘制成两幅不完整的统计图
:差)四类.依据调查结果绘制成两幅不完整的统计图
(1)这次被调查的学生一共有 人,其中![]() (中)等次的男生有 人,表示
(中)等次的男生有 人,表示![]() (差)等次的扇形所对的圆心角的度数为 度;
(差)等次的扇形所对的圆心角的度数为 度;
(2)若该校约有![]() 名学生,估计全校居家学习处于优或良(
名学生,估计全校居家学习处于优或良(![]() 或
或![]() )等次的学生有多少人?
)等次的学生有多少人?
(3)为了共同进步,刘老师想从被调查的![]() 类和
类和![]() 类学生中分别选取一位同学进行“一对—”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位男同学的概率.
类学生中分别选取一位同学进行“一对—”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位男同学的概率.
【答案】(1)![]() ;(2)920人;(3)树状图见解析,
;(2)920人;(3)树状图见解析,![]()
【解析】
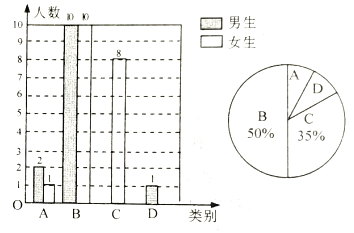
(1)依据B类的学生人数以及百分比即可得到调查的学生人数,C类的学生人数为40×35%=14(人),其中男生有14-8=6(人),D类学生人数为40×7.5%=3(人),再用360°乘以D等次人数所占比例即得;
(2)总人数乘以A、B等次人数和所占比例即可得;
(3)根据树状图可得,共有9种等可能的结果,其中所选的两位同学恰好是两位男同学的情况有2种,即可得到所选的两位同学恰好是两位男同学的概率.
解:(1)这次被调查的学生一共有(10+10)÷50%=40(人),
其中C(中)等次的男生有40×35%-8=6(人),
D等级人数为40-(3+20+14)=3(人)
∴表示D(差)等次的扇形所对的圆心角的度数为![]() ,
,
故答案为:40、6、27;
(2)估计全校居家学习处于优或良(A或B)等次的学生有1600×![]() (人);
(人);
(3)画树状图如下: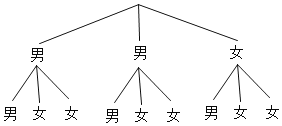
共有9种等可能的结果,其中所选的两位同学恰好是两位男同学的情况有2种,
∴所选的两位同学恰好是两位男同学的概率为![]() .
.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】袋中有四张卡片,其中两张红色卡片![]() ,标号分别为
,标号分别为![]() ;两张蓝色卡片
;两张蓝色卡片![]() ,标号分别为
,标号分别为![]() .
.
(1)从以上四张卡片中任取两张,求这两张卡片颜色不同且标号之和小于![]() 的概率;
的概率;
(2)向袋中再放入一张绿色卡片![]() ,标号记为
,标号记为![]() ,从这五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于
,从这五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
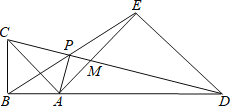
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.
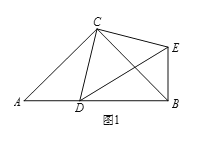
填空: ①![]() 的值为 ;②∠DBE的度数为 .
的值为 ;②∠DBE的度数为 .
(2)类比探究
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由.
的值及∠DBE的度数,并说明理由.
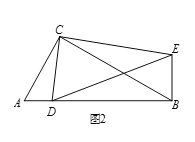
(3)拓展延伸
如面3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
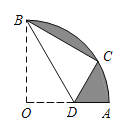
【题目】如图,在扇形AOB中,∠AOB=90°,半径OA=4.将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点C处,折痕交OA于点D,则图中阴影部分的面积为_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com