
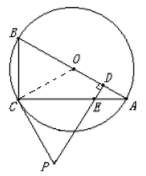
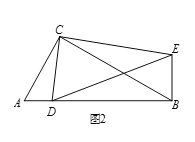
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P.
(1)求证:PC=PE;
(2)求证:PC是⊙O的切线;
(3)若AB=10,AD=2,AE=![]() ,求PC的长.
,求PC的长.

【答案】(1)详见解析;(2)详见解析;(3)PC=![]()
【解析】
(1)由等角对等边,即可得到结论成立;
(2)连接OC,则∠AED+∠OAC=90°,结合(1)的结论,得到PC⊥OC,即可得到结论成立;
(3)由题意,先求出DE的长度,然后由△ABC∽△AED,求出BC,从而得到AC,再由相似三角形的性质,即可求出PC的长度.
证明:(1)∵∠AED=∠CEP,∠ECP=∠AED,
∴∠ECP=∠CEP,
∴PC=PE.
(2)如图,连接OC,则OC=OA,
∴∠OCA=∠OAC,
∵PD⊥AB,
∴∠AED+∠OAC=90°,
由(1)知∠ECP+∠OCA=∠ECP+∠OAC=90°即PC⊥OC,
∴PC是⊙O的切线.
(3)解:∵PD⊥AB,在Rt△AED中,
∴DE=![]() ,
,
∵∠A=∠A,∠ADE=∠ACB=90°,
∴△ABC∽△AED,
∴![]() ,把AB=10,AE=
,把AB=10,AE=![]() ,DE=
,DE=![]() 代入,
代入,
∴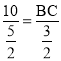
∴BC=6,
由勾股定理求得:AC=8.
∵∠PCE+∠OCE=∠OCB+∠OCE=90°,
∴∠PCE=∠OCB,
由(2)知等腰△PCE∽△OCB,有![]() ,
,
即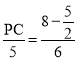 ,
,
∴PC=![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
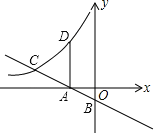
【题目】如图,直线y=-![]() x-
x-![]() 与x,y两轴分别交于A,B两点,与反比例函数y=
与x,y两轴分别交于A,B两点,与反比例函数y=![]() 的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,折叠矩形纸片 ABCD,具体操作:①点 E 为 AD 边上一点(不与点 A,D 重合),把△ABE 沿 BE 所在的直线折叠,A 点的对称点为 F 点;②过点 E 对折∠DEF,折痕EG 所在的直线交 DC 于点 G,D 点的对称点为 H 点.
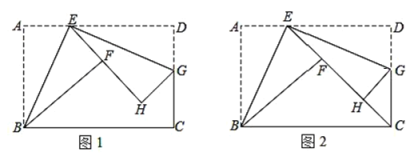
(1)求证:△ABE∽△DEG.
(2)若 AB=6,BC=10
①点 E 在移动的过程中,求 DG 的最大值;
②如图 2,若点 C 恰在直线 EF 上,连接 DH,求线段 DH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深两寸,锯道长八寸,问径几何?”用现代的数学语言表述是:“![]() 为
为![]() 的直径,弦
的直径,弦![]() ,垂足为点
,垂足为点![]() ,
,![]() 寸,
寸,![]() 寸,求直径
寸,求直径![]() 的长?”依题意
的长?”依题意![]() 的长为( )
的长为( )
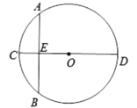
A.6寸B.8寸C.10寸D.12寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中有四张卡片,其中两张红色卡片![]() ,标号分别为
,标号分别为![]() ;两张蓝色卡片
;两张蓝色卡片![]() ,标号分别为
,标号分别为![]() .
.
(1)从以上四张卡片中任取两张,求这两张卡片颜色不同且标号之和小于![]() 的概率;
的概率;
(2)向袋中再放入一张绿色卡片![]() ,标号记为
,标号记为![]() ,从这五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于
,从这五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒令是中国民间风俗之一.白居易曾诗曰:“花时同醉破春愁,醉折花枝当酒筹”饮酒行令,是中国人在饮酒时助兴的一种特有方式,不仅要以酒助兴,往往还伴之以赋诗填词、猜迷形拳之举,最早诞生于西周,完备于隋唐,“虎棒鸡虫令”是其中一种:“二人相对,以筷子相声,同时或喊虎、喊棒、喊鸡、喊虫,以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负,负者饮.若棒兴鸡、或虫兴虎同时出现(解释:若棒与鸡,虎与虫同时喊出)或两人喊出同一物,则不分胜负,继续喊”.依据上述规则,张三和李四同时随机地喊出其中一物,两人只喊一次.
(1)求张三喊出“虎”取胜的概率;
(2)用列表法或画树状图法,求李四取胜的概率;
(3)直接写出两人能分出胜负的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A、B,与y轴负半轴交于点C,且OC=OB,其中B点坐标为(3,0),对称轴l为直线x=![]() .
.
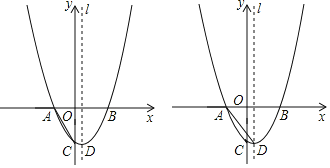
(1)求抛物线的解析式;
(2)在x轴上方有一点P,连接PA后满足∠PAB=∠CAB,记△PBC的面积为S,求当S=10.5时点P的坐标;
(3)在(2)的条件下,当点P恰好落在抛物线上时,将直线BC上下平移,平移后的直线y=x+t与抛物线交于C′、B′两点(C′在B′的左侧),若以点C′、B′、P为顶点的三角形是直角三角形,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.
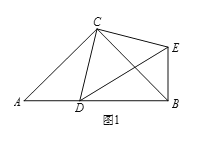
填空: ①![]() 的值为 ;②∠DBE的度数为 .
的值为 ;②∠DBE的度数为 .
(2)类比探究
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由.
的值及∠DBE的度数,并说明理由.
(3)拓展延伸
如面3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com