
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A、B,与y轴负半轴交于点C,且OC=OB,其中B点坐标为(3,0),对称轴l为直线x=![]() .
.
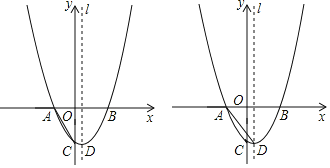
(1)求抛物线的解析式;
(2)在x轴上方有一点P,连接PA后满足∠PAB=∠CAB,记△PBC的面积为S,求当S=10.5时点P的坐标;
(3)在(2)的条件下,当点P恰好落在抛物线上时,将直线BC上下平移,平移后的直线y=x+t与抛物线交于C′、B′两点(C′在B′的左侧),若以点C′、B′、P为顶点的三角形是直角三角形,求出t的值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3;(2)点P(2,6);(3)19或32
x﹣3;(2)点P(2,6);(3)19或32
【解析】
(1)先确定出点A坐标,再用待定系数法即可得出结论;
(2)先确定出直线AP的解析式,进而用m表示点P的坐标,即可求出S与m的函数关系,即可求出答案;
(3)先确定出点P的坐标,当∠B'PC'=90°时,利用根与系数的关系确定出B'C'的中点E的坐标,利用B'C'=2PE建立方程求解,当∠PC'B'=90°时,先确定出点G的坐标,进而求出直线C'G的解析式,进而得出点C'的坐标,即可得出结论.
解:(1)∵B(3,0),对称轴为直线x=![]() ,
,
∴A(﹣2,0),
∴抛物线的解析式为y=a(x+2)(x﹣3)=ax2﹣ax﹣6a,
∵B(3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴C(0,﹣3),
把C(0,﹣3)代入y=a(x+2)(x﹣3),
得:﹣6a=﹣3,
∴a=![]() ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣3;
x﹣3;
(2)如图1,射线AP与y轴的交点记作点C',
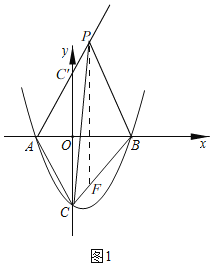
∵∠BAC=∠BAC',OA=OA,∠AOC=∠AOC'=90°,
∴△AOC≌△AOC'(ASA),
∴OC'=OC=3,
∴C'(0,3),
∵A(﹣2,0),
设直线AP的解析式为y=kx+b,
把A,C'两点代入得![]() ,
,
解得:![]() ,
,
∴直线AP的解析式为y=![]() x+3,
x+3,
∵点P(m,n)在直线AP上,
∴n=![]() m+3,
m+3,
∵B(3,0),C(0,﹣3),
∴直线BC的解析式为y=k1x﹣3,
∴0=3k1﹣3,
解得:k1=1,
∴直线BC的解析式为y=x﹣3,
过点P作y轴的平行线交BC于F,
∴F(m,m﹣3),
∴PF=![]() m+3﹣(m﹣3)=
m+3﹣(m﹣3)=![]() m+6,
m+6,
∴S=S△PBC=![]() OBPF=
OBPF=![]() ×3(
×3(![]() m+6)=
m+6)=![]() m+9(m>﹣2);
m+9(m>﹣2);
∴当S=10.5时,10.5=![]() m+9,
m+9,
∴m=2,
∴点P(2,6);
(3)由(1)知,抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣3①
x﹣3①
由(2)知,直线AP的解析式为y=![]() x+3②,
x+3②,
联立①②解得,![]() 或
或![]() ,
,
∴P(6,12),
如图2,
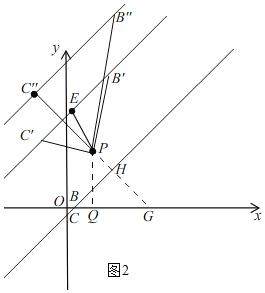
当∠C'PB'=90°时,取B'C'的中点E,连接PE,
则B'C'=2PE,即:B'C'2=4PE2,
设B'(x1,y1),C'(x2,y2),
∵直线B'C'的解析式为y=x+t③,
联立①③化简得,x2﹣3x﹣(2t+6)=0,
∴x1+x2=3,x1x2=﹣(2t+6),
∴点E(![]() ,
,![]() +t),
+t),
B'C'2=(x1﹣x2)2+(y1﹣y2)2=2(x1﹣x2)2=2[(x1+x2)2﹣4x1x2]=2[9+4(2t+6)]=16t+66,
而PE2=(6﹣![]() )2+(12﹣
)2+(12﹣![]() ﹣t)2=t2﹣21t+
﹣t)2=t2﹣21t+![]() ,
,
∴16t+66=4(t2﹣21t+![]() ),
),
∴t=6(此时,恰好过点P,舍去)或t=19,
当∠PC'B'=90°时,延长C'P交BC于H,交x轴于G,
则∠BHC=90°,
∵OB=CO,∠BOC=90°,
∴∠OBC=45°,
∴∠PGO=45°,
过点P作PQ⊥x轴于Q,则GQ=PQ=12,
∴OG=OQ+GQ=18,
∴点G(18,0),
∴直线C'G的解析式为y=﹣x+18④,
联立①④解得![]() 或
或![]() ,
,
∴C'的坐标为(﹣7,25),
将点C'坐标代入y=x+t中,得25=﹣7+t,
∴t=32,
即:满足条件的t的值为19或32.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为![]() ,点C的坐标为
,点C的坐标为![]() .
.
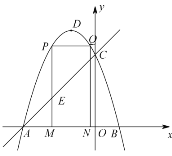
(Ⅰ)求抛物线的解析式;
(Ⅱ)点M为线段![]() 上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线
上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线![]() 交于点E,与抛物线交于点P,过点P作
交于点E,与抛物线交于点P,过点P作![]() 交抛物线于点Q,过点Q作
交抛物线于点Q,过点Q作![]() 轴于点N.若点P在点Q左边,当矩形
轴于点N.若点P在点Q左边,当矩形![]() 的周长最大时,求
的周长最大时,求![]() 的面积;
的面积;
(Ⅲ)在(Ⅱ)的条件下,当矩形![]() 的周长最大时,连接
的周长最大时,连接![]() ,过抛物线上一点F作y轴的平行线,与直线
,过抛物线上一点F作y轴的平行线,与直线![]() 交于点G(点G在点F的上方).若
交于点G(点G在点F的上方).若![]() ,求点F的坐标.
,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P.
(1)求证:PC=PE;
(2)求证:PC是⊙O的切线;
(3)若AB=10,AD=2,AE=![]() ,求PC的长.
,求PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠病毒(2019-nCoV是一种新的Sarbecovirus亚属的![]() 冠状病毒,它是一类具有囊膜的正链单股RNA病毒,其遗传物质是所有RNA病毒中最大的,也是自然界广泛存在的一大类病毒,其粒子形状并不规则,直径约60~220nm,平均直径为100nm(纳米).
冠状病毒,它是一类具有囊膜的正链单股RNA病毒,其遗传物质是所有RNA病毒中最大的,也是自然界广泛存在的一大类病毒,其粒子形状并不规则,直径约60~220nm,平均直径为100nm(纳米).![]() ,100nm用科学记数法可以表示为( )m.
,100nm用科学记数法可以表示为( )m.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难,八方支援.“新冠肺炎”疫情来袭,除了医务人员主动请缨逆行走向战场外,众多企业也伸出援助之手.某公司用甲,乙两种货车向武汉运送爱心物资,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运物资吨数 | |
第一次 | 3 | 4 | 29 |
第二次 | 2 | 6 | 31 |
(1)求甲、乙两种货车每次满载分别能运输多少吨物资;
(2)目前有46.4吨物资要运输到武汉,该公司拟安排甲乙货车共10辆,全部物资一次运完,其中每辆甲车一次运送花费500元,每辆乙车一次运送花费300元,请问该公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
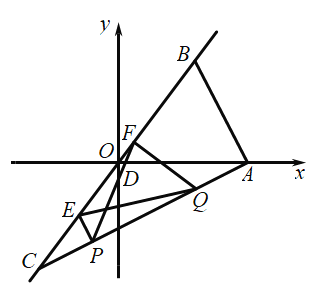
【题目】如图,在平面直角坐标系中,![]() 的斜边
的斜边![]() 在直线
在直线![]() 上,且
上,且![]() 是
是![]() 的中点,点
的中点,点![]() 的坐标为
的坐标为![]() .点
.点![]() 在线段
在线段![]() 上从
上从![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上从
上从![]() 点向
点向![]() 点运动,且
点运动,且![]() .
.
(1)求![]() 的长及点
的长及点![]() 的坐标.
的坐标.
(2)作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,设
,设![]() .
.
①在![]() ,
,![]() 相遇前,用含
相遇前,用含![]() 的代数式表示
的代数式表示![]() 的长.
的长.
②当![]() 为何值时,
为何值时,![]() 与坐标轴垂直.
与坐标轴垂直.
(3)若![]() 交
交![]() 轴于点
轴于点![]() ,除点
,除点![]() 与点
与点![]() 重合外,
重合外,![]() 的值是否为定值,若是,请直接写出
的值是否为定值,若是,请直接写出![]() 的值,若不是,请直接写出它的取值范围.
的值,若不是,请直接写出它的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.
(1)求每次降价的百分率.
(2)若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
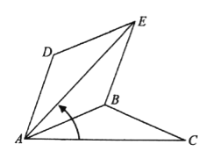
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连结
,连结![]() .
.
(1)求证:![]() ;
;
(2)四边形![]() 是什么形状的四边形?并说明理由;
是什么形状的四边形?并说明理由;
(3)直接写出:当![]() 分别是多少度时,①
分别是多少度时,①![]() ;②
;②![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com