
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为![]() ,点C的坐标为
,点C的坐标为![]() .
.
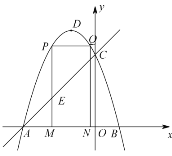
(Ⅰ)求抛物线的解析式;
(Ⅱ)点M为线段![]() 上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线
上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线![]() 交于点E,与抛物线交于点P,过点P作
交于点E,与抛物线交于点P,过点P作![]() 交抛物线于点Q,过点Q作
交抛物线于点Q,过点Q作![]() 轴于点N.若点P在点Q左边,当矩形
轴于点N.若点P在点Q左边,当矩形![]() 的周长最大时,求
的周长最大时,求![]() 的面积;
的面积;
(Ⅲ)在(Ⅱ)的条件下,当矩形![]() 的周长最大时,连接
的周长最大时,连接![]() ,过抛物线上一点F作y轴的平行线,与直线
,过抛物线上一点F作y轴的平行线,与直线![]() 交于点G(点G在点F的上方).若
交于点G(点G在点F的上方).若![]() ,求点F的坐标.
,求点F的坐标.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]()
【解析】
(Ⅰ)将点A,点C坐标代入解析式可求解;
(Ⅱ)设M(x,0),P(x,-x2-2x+3),利用对称性可求点Q(-2-x,-x2-2x+3),可求MP=-x2-2x+3,PQ=-2-x-x=-2-2x,则可用x表示矩形PMNQ的周长,由二次函数的性质可求当矩形PMNQ的周长最大时,点P的坐标,即可求点E,点M的坐标,由三角形面积公式可求解;
(Ⅲ)先求出点D坐标,即可求DQ=![]() ,可得FG=4,设F (m,-m2-2m+3),则G (m,m+3),用含有m的式子表示FG的长度即可求解.
,可得FG=4,设F (m,-m2-2m+3),则G (m,m+3),用含有m的式子表示FG的长度即可求解.
解:(Ⅰ)依题意
解得![]()
所以![]()
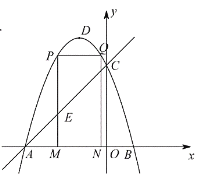
(Ⅱ)![]()
抛物线的对称轴是直线![]()
![]() ,
,![]() ,其中
,其中![]()
∵P、Q关于直线![]() 对称
对称
设Q的横坐标为a
则![]()
∴![]()
∴![]()
∴![]() ,
,![]()
∴周长![]()
当![]() 时,d取最大值,此时,
时,d取最大值,此时,![]()
∴![]()
设直线![]() 的解析式为
的解析式为![]()
则![]() ,解得
,解得![]()
∴设直线![]() 的解析式为
的解析式为![]()
将![]() 代入
代入![]() ,得
,得![]()
∴![]() ,
,
∴![]()
∴![]()
(Ⅲ)由(Ⅱ)知,当矩形![]() 的周长最大时,
的周长最大时,![]() 此时点
此时点![]() ,与点C重合,
,与点C重合,
∴![]()
∵![]()
∴![]()
过D作![]() 轴于K,
轴于K,
则![]() ,
,![]()
∴![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
设![]() ,则
,则![]()
![]()
∴![]() ,解得
,解得![]() ,
,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() .
.
∴![]() 或
或![]()



科目:初中数学 来源: 题型:
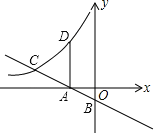
【题目】如图,直线y=-![]() x-
x-![]() 与x,y两轴分别交于A,B两点,与反比例函数y=
与x,y两轴分别交于A,B两点,与反比例函数y=![]() 的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
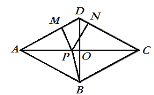
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,折叠矩形纸片 ABCD,具体操作:①点 E 为 AD 边上一点(不与点 A,D 重合),把△ABE 沿 BE 所在的直线折叠,A 点的对称点为 F 点;②过点 E 对折∠DEF,折痕EG 所在的直线交 DC 于点 G,D 点的对称点为 H 点.
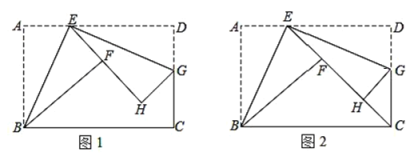
(1)求证:△ABE∽△DEG.
(2)若 AB=6,BC=10
①点 E 在移动的过程中,求 DG 的最大值;
②如图 2,若点 C 恰在直线 EF 上,连接 DH,求线段 DH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深两寸,锯道长八寸,问径几何?”用现代的数学语言表述是:“![]() 为
为![]() 的直径,弦
的直径,弦![]() ,垂足为点
,垂足为点![]() ,
,![]() 寸,
寸,![]() 寸,求直径
寸,求直径![]() 的长?”依题意
的长?”依题意![]() 的长为( )
的长为( )
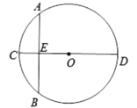
A.6寸B.8寸C.10寸D.12寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A、B,与y轴负半轴交于点C,且OC=OB,其中B点坐标为(3,0),对称轴l为直线x=![]() .
.
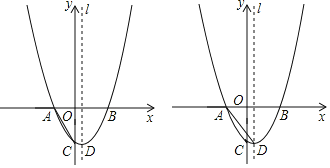
(1)求抛物线的解析式;
(2)在x轴上方有一点P,连接PA后满足∠PAB=∠CAB,记△PBC的面积为S,求当S=10.5时点P的坐标;
(3)在(2)的条件下,当点P恰好落在抛物线上时,将直线BC上下平移,平移后的直线y=x+t与抛物线交于C′、B′两点(C′在B′的左侧),若以点C′、B′、P为顶点的三角形是直角三角形,求出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com