
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() 是以点
是以点![]() 为圆心,
为圆心,![]() 为半径的圆上的动点,
为半径的圆上的动点,![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,则线段
,则线段![]() 的最小值是( )
的最小值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)

(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条直线把矩形分割成两个矩形,其中一个为黄金矩形 (宽与长的比为![]() 的矩形),则称这条直线为该矩形的黄金线.例如图所示的矩形
的矩形),则称这条直线为该矩形的黄金线.例如图所示的矩形![]() 中,直线
中,直线![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,显然直线
,显然直线![]() 是矩形
是矩形![]() 的黄金线.
的黄金线.
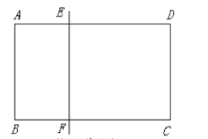
(1)如图,在矩形![]() 中,
中,![]() ,
,![]() .请在图中画出矩形
.请在图中画出矩形![]() 的其中一条黄金线
的其中一条黄金线![]() ,其中
,其中![]() 在
在![]() 边上,
边上,![]() 在
在![]() 边上,并标注出线段
边上,并标注出线段![]() 的长度;
的长度;
(2)将正方形纸片按图所示的方式折叠.
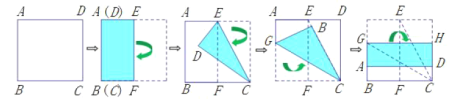
如图所示,按上述方法折叠所得到的折痕![]() 是否为正方形
是否为正方形![]() 的黄金线?请说明理由.
的黄金线?请说明理由.
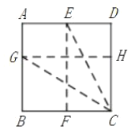
(3)在矩形![]() 中,
中,![]() ,
,![]() ,己知矩形
,己知矩形![]() 的黄金线
的黄金线![]() 恰好将矩形
恰好将矩形![]() 分割成两个黄金矩形,则
分割成两个黄金矩形,则![]() ______(只要求直接写出其中三个答案).
______(只要求直接写出其中三个答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年初,一场突如其来的冠状肺炎肆虐全国,学生经历了“停课不停学”,疫情逐渐消退.某校在开学前夕,准备买一批酒精和
年初,一场突如其来的冠状肺炎肆虐全国,学生经历了“停课不停学”,疫情逐渐消退.某校在开学前夕,准备买一批酒精和![]() 消毒液对校园进行消毒,经调查,若购买
消毒液对校园进行消毒,经调查,若购买![]() 箱酒精和
箱酒精和![]() 箱
箱![]() 消毒液共需
消毒液共需![]() 元,购买
元,购买![]() 箱酒精和
箱酒精和![]() 箱
箱![]() 消毒液共需
消毒液共需![]() 元.
元.
(1)求酒精和![]() 消毒液的单价;
消毒液的单价;
(2)根据学校实际情况,需从该商店一次性购买酒精和![]() 消毒液共
消毒液共![]() 箱,总费用不超过
箱,总费用不超过![]() 元,那么最多可以购买多少箱
元,那么最多可以购买多少箱![]() 消毒液?
消毒液?
(3)由于分阶段开学,九年级学生第一批开学,年级组长张老师准备用![]() 元购买一批酒精和
元购买一批酒精和![]() 消毒液进行先期消毒,在钱刚好用完的条件下,他有哪几种购买方案?
消毒液进行先期消毒,在钱刚好用完的条件下,他有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
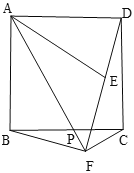
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为![]() ,点C的坐标为
,点C的坐标为![]() .
.
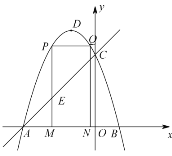
(Ⅰ)求抛物线的解析式;
(Ⅱ)点M为线段![]() 上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线
上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线![]() 交于点E,与抛物线交于点P,过点P作
交于点E,与抛物线交于点P,过点P作![]() 交抛物线于点Q,过点Q作
交抛物线于点Q,过点Q作![]() 轴于点N.若点P在点Q左边,当矩形
轴于点N.若点P在点Q左边,当矩形![]() 的周长最大时,求
的周长最大时,求![]() 的面积;
的面积;
(Ⅲ)在(Ⅱ)的条件下,当矩形![]() 的周长最大时,连接
的周长最大时,连接![]() ,过抛物线上一点F作y轴的平行线,与直线
,过抛物线上一点F作y轴的平行线,与直线![]() 交于点G(点G在点F的上方).若
交于点G(点G在点F的上方).若![]() ,求点F的坐标.
,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为6,点A,B,C为⊙O上三点,BA平分∠OBC,过点A作AD⊥BC交BC延长线于点D.
(1)求证:AD是⊙O的切线;
(2)当sin∠OBC=![]() 时,求BC的长;
时,求BC的长;
(3)连结AC,当AC∥OB时,求图中阴影部分的面积.
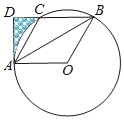
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠病毒(2019-nCoV是一种新的Sarbecovirus亚属的![]() 冠状病毒,它是一类具有囊膜的正链单股RNA病毒,其遗传物质是所有RNA病毒中最大的,也是自然界广泛存在的一大类病毒,其粒子形状并不规则,直径约60~220nm,平均直径为100nm(纳米).
冠状病毒,它是一类具有囊膜的正链单股RNA病毒,其遗传物质是所有RNA病毒中最大的,也是自然界广泛存在的一大类病毒,其粒子形状并不规则,直径约60~220nm,平均直径为100nm(纳米).![]() ,100nm用科学记数法可以表示为( )m.
,100nm用科学记数法可以表示为( )m.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com