
【题目】![]() 年初,一场突如其来的冠状肺炎肆虐全国,学生经历了“停课不停学”,疫情逐渐消退.某校在开学前夕,准备买一批酒精和
年初,一场突如其来的冠状肺炎肆虐全国,学生经历了“停课不停学”,疫情逐渐消退.某校在开学前夕,准备买一批酒精和![]() 消毒液对校园进行消毒,经调查,若购买
消毒液对校园进行消毒,经调查,若购买![]() 箱酒精和
箱酒精和![]() 箱
箱![]() 消毒液共需
消毒液共需![]() 元,购买
元,购买![]() 箱酒精和
箱酒精和![]() 箱
箱![]() 消毒液共需
消毒液共需![]() 元.
元.
(1)求酒精和![]() 消毒液的单价;
消毒液的单价;
(2)根据学校实际情况,需从该商店一次性购买酒精和![]() 消毒液共
消毒液共![]() 箱,总费用不超过
箱,总费用不超过![]() 元,那么最多可以购买多少箱
元,那么最多可以购买多少箱![]() 消毒液?
消毒液?
(3)由于分阶段开学,九年级学生第一批开学,年级组长张老师准备用![]() 元购买一批酒精和
元购买一批酒精和![]() 消毒液进行先期消毒,在钱刚好用完的条件下,他有哪几种购买方案?
消毒液进行先期消毒,在钱刚好用完的条件下,他有哪几种购买方案?
【答案】(1)每箱酒精50元,每箱84消毒液80元;(2)最多可以买33箱84消毒液;(3)共有2种购买方案,方案一:购买酒精12箱、84消毒液5箱;方案二:购买酒精4箱、84消毒液10箱
【解析】
(1)设每箱酒精x元,每箱84消毒液y元,根据“购买1箱酒精和2箱84消毒液共需210元,购买2箱酒精和5箱84消毒液共需500元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买84消毒液![]() 箱,则购买酒精(
箱,则购买酒精(![]() )箱,根据“总价=单价×数量”结合购买酒精和84消毒液的总费用不超过4000元,即可得出关于
)箱,根据“总价=单价×数量”结合购买酒精和84消毒液的总费用不超过4000元,即可得出关于![]() 的一元一次不等式,解之取其中的最大值整数值即可得出结论;
的一元一次不等式,解之取其中的最大值整数值即可得出结论;
(3)设购买酒精![]() 箱,购买84消毒液
箱,购买84消毒液![]() 箱,根据“总价=单价×数量”结合总价为1000元,即可得出关于
箱,根据“总价=单价×数量”结合总价为1000元,即可得出关于![]() ,
,![]() 的二元一次方程,结合
的二元一次方程,结合![]() ,
,![]() 均为非负整数,即可得出各购买方案.
均为非负整数,即可得出各购买方案.
(1)设每箱酒精x元,每箱84消毒液y元,
依题意,得:![]() ,
,
解得:![]() .
.
答:每箱酒精50元,每箱84消毒液80元;
(2)设购买84消毒液![]() 箱,则购买酒精(
箱,则购买酒精(![]() )箱,
)箱,
依题意,得:![]() +50(
+50(![]() )≤4000,
)≤4000,
解得:![]() .
.
∵![]() 为整数,
为整数,
∴![]() 最大取33,
最大取33,
答:最多可以买33箱84消毒液;
(3)设购买酒精![]() 箱,购买84消毒液
箱,购买84消毒液![]() 箱,
箱,
依题意,得:![]() ,
,
∴![]() .
.
∵![]() ,
,![]() 均为非负整数,且都需购买,
均为非负整数,且都需购买,
∴![]() 5或10.
5或10.
∴共有2种购买方案,方案一:购买酒精12箱、84消毒液5箱;方案二:购买酒精4箱、84消毒液10箱.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
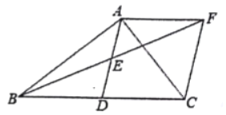
【题目】如图,在![]() 中,
中,![]() ,AD是BC边上的中线,点E为AD的中点,过点A作
,AD是BC边上的中线,点E为AD的中点,过点A作![]() 交BE的延长线于点F,连接CF.
交BE的延长线于点F,连接CF.
(1)求证:![]() ;
;
(2)连接DF,当![]() 度时,四边形ABDF为菱形?证明你的结论.
度时,四边形ABDF为菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化校园,学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉30盆,搭配一个B种造型需甲种花卉40盆,乙种花卉80盆.则符合要求的搭配方案有几种( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
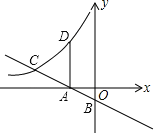
【题目】如图,直线y=-![]() x-
x-![]() 与x,y两轴分别交于A,B两点,与反比例函数y=
与x,y两轴分别交于A,B两点,与反比例函数y=![]() 的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
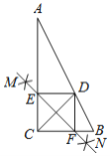
【题目】如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于![]() 的长为半径作弧,两弧相交于M,N两点;
的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,折叠矩形纸片 ABCD,具体操作:①点 E 为 AD 边上一点(不与点 A,D 重合),把△ABE 沿 BE 所在的直线折叠,A 点的对称点为 F 点;②过点 E 对折∠DEF,折痕EG 所在的直线交 DC 于点 G,D 点的对称点为 H 点.
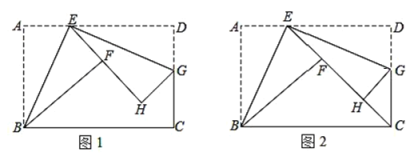
(1)求证:△ABE∽△DEG.
(2)若 AB=6,BC=10
①点 E 在移动的过程中,求 DG 的最大值;
②如图 2,若点 C 恰在直线 EF 上,连接 DH,求线段 DH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒令是中国民间风俗之一.白居易曾诗曰:“花时同醉破春愁,醉折花枝当酒筹”饮酒行令,是中国人在饮酒时助兴的一种特有方式,不仅要以酒助兴,往往还伴之以赋诗填词、猜迷形拳之举,最早诞生于西周,完备于隋唐,“虎棒鸡虫令”是其中一种:“二人相对,以筷子相声,同时或喊虎、喊棒、喊鸡、喊虫,以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负,负者饮.若棒兴鸡、或虫兴虎同时出现(解释:若棒与鸡,虎与虫同时喊出)或两人喊出同一物,则不分胜负,继续喊”.依据上述规则,张三和李四同时随机地喊出其中一物,两人只喊一次.
(1)求张三喊出“虎”取胜的概率;
(2)用列表法或画树状图法,求李四取胜的概率;
(3)直接写出两人能分出胜负的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com