
【题目】已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0.
![]()
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:|x+1|-|x-1|+2|x+5|(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1)-1;1;5;(2)4x+10或2x+12.;(3)不变,理由见解析.
【解析】
(1)根据b是最小的正整数,即可确定b的值,然后根据非负数的性质,几个非负数的和是0,则每个数是0,即可求得a,b,c的值;
(2)根据x的范围,确定x+1,x-3,5-x的符号,然后根据绝对值的意义即可化简;
(3)先求出BC=3t+4,AB=3t+2,从而得出BC-AB=2.
(1)∵b是最小的正整数,∴b=1.
根据题意得:c-5=0且a+b=0,
∴a=-1,b=1,c=5.
故答案是:-1;1;5;
(2)当0≤x≤1时,x+1>0,x-1≤0,x+5>0,
则:|x+1|-|x-1|+2|x+5|
=x+1-(1-x)+2(x+5)
=x+1-1+x+2x+10
=4x+10;
当1<x≤2时,x+1>0,x-1>0,x+5>0.
∴|x+1|-|x-1|+2|x+5|=x+1-(x-1)+2(x+5)
=x+1-x+1+2x+10
=2x+12;
(3)不变.理由如下:
t秒时,点A对应的数为-1-t,点B对应的数为2t+1,点C对应的数为5t+5.
∴BC=(5t+5)-(2t+1)=3t+4,AB=(2t+1)-(-1-t)=3t+2,
∴BC-AB=(3t+4)-(3t+2)=2,
即BC-AB的不随着时间t的变化而改变.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”。图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速,设运动的时间为t秒,问:
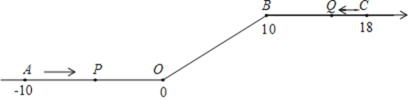
(1)动点P从点A运动至点C需要________秒;
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少?
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
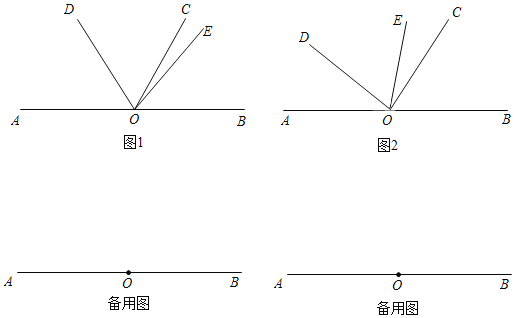
【题目】已知O为直线AB上一点,射线OD、OC、OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=α.
(1)如图1,α=70°,当OD平分∠AOC时,求∠EOB的度数.
(2)如图2,若∠DOC=2∠AOD,且α<80°,求∠EOB的度数(用含α的代数式表示);
(3)若α=90°,点F在射线OB上,若射线OF绕点O顺时针旋转n°(0<n<180),∠FOA=2∠AOD,OH平分∠EOC,当∠FOH=∠AOC时,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
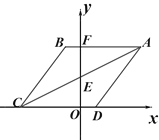
【题目】如图O为坐标原点,四边形ABCD是菱形,A(4,4),B点在第二象限,AB=5,AB与y轴交于点F,对角线AC交y轴于点E
(1)直接写出B、C点的坐标;
(2)动点P从C点出发以每秒1个单位的速度沿折线段C﹣D﹣A运动,设运动时间为t秒,请用含t的代数式表示△EDP的面积;
(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形?若存在,请直接写出当t为多少秒时存在符合条件的点P;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=2,BC=4.点D是线段BC上的一个动点.点D与点B、C不重合,过点D作DE⊥BC交AB于点E,将△ABC沿着直线DE翻折,使点B落在直线BC上的F点.
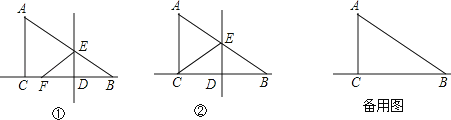
(1)设∠BAC=α(如图①),求∠AEF的大小;(用含α的代数式表示)
(2)当点F与点C重合时(如图②),求线段DE的长度;
(3)设BD=x,△EDF与△ABC重叠部分的面积为S,试求出S与x之间函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 所示,用 20 m 的篱笆(细线部分),两面靠墙围成矩形的苗圃.
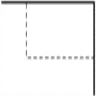
(1)设矩形的一边长为x(m),面积为y(m 2 ),求y关于x的函数表达式;
(2)求当x取8、9、10、11、12时y的值,并观察这几种情况下,哪种情况面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
(1)求证:△ABD∽△CBA;
(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com