
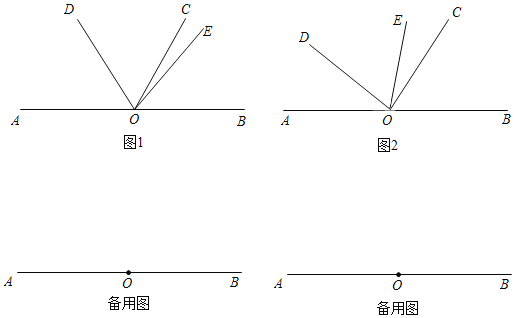
【题目】已知O为直线AB上一点,射线OD、OC、OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=α.
(1)如图1,α=70°,当OD平分∠AOC时,求∠EOB的度数.
(2)如图2,若∠DOC=2∠AOD,且α<80°,求∠EOB的度数(用含α的代数式表示);
(3)若α=90°,点F在射线OB上,若射线OF绕点O顺时针旋转n°(0<n<180),∠FOA=2∠AOD,OH平分∠EOC,当∠FOH=∠AOC时,求n的值.
【答案】(1)10°;(2)140°﹣α;(3)OF旋转的角度为72°或者168°.
【解析】
(1)根据角平分线的定义即可得到结论;
(2)根据角的和差即可得到结论;
(3)①当∠DOE在∠AOC内部,当∠DOE在射线OC的两侧,根据题意列方程即可得到结论.
解:(1)∵OD平分∠AOC,
∴∠AOD=∠COD=60°,
∵∠DOE=70°,
∴∠COE=10°,
∴∠EOB=180°﹣120°﹣10°=50°;
(2)∵∠DOC=2∠COE,
∴∠DOC=80°,
∴∠EOC=80°﹣α,
∵∠COB=60°,
∴∠EOB=140°﹣α;
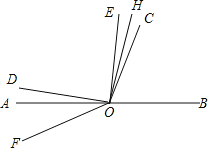
(3)①当∠DOE在∠AOC内部,
令∠AOD=x°,则∠AOF=2x°,
∠EOC=120﹣x°﹣90°=30°﹣x°,
∠EOH=![]() (30°﹣x),
(30°﹣x),
∴∠HOF=![]() (30°﹣x)+90°+x°+2 x°=120°,
(30°﹣x)+90°+x°+2 x°=120°,
解得:x=6,
则∠BOF=180°﹣2x=168°;
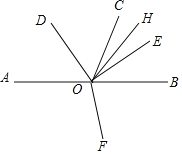
②当∠DOE在射线OC的两侧,
令∠AOD=x°,则∠AOF=2x°,∠COD=120﹣x°,
∠EOC=90°﹣(120﹣x°)=x°﹣30°,
∠EOH=![]() (x°﹣30°),
(x°﹣30°),
∠EOB=90°﹣x°,∠BOF=180°﹣2x,
∴∠HOF=![]() (x°﹣30°)+90°﹣x+180°﹣2x=120°,
(x°﹣30°)+90°﹣x+180°﹣2x=120°,
解得:x=54,
则∠BOF=180°﹣2x=72°,
综上所述得:OF旋转的角度为72°或者168°.


科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
0.275,﹣|﹣2|,﹣1.04,﹣(﹣10)2,﹣(﹣8), -![]() ,0,﹣
,0,﹣![]() .
.
负数集合{ …};
非负整数集合{ …};
整数集合{ …};
分数集合{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动;第1次点A向左移动3个单位长度至点![]() ,第2次从点
,第2次从点![]() 向右移动6个单位长度至点
向右移动6个单位长度至点![]() ,第3次从点
,第3次从点![]() 向左移动9个单位长度至点
向左移动9个单位长度至点![]() ,…,按照这种移动方式进行下去,如果点
,…,按照这种移动方式进行下去,如果点![]() 与原点的距离不小于20,那么n的最小值是________.
与原点的距离不小于20,那么n的最小值是________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
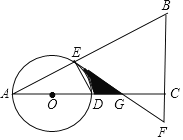
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
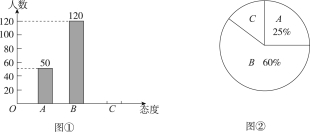
【题目】中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者随机调查了某市城区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成),并将调査结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调査中,共调査了 名中学生家长;
(2)将图①补充完整;
(3)根据抽样调查结果,请你估计该市城区80 000名中学生家长中有多少名家长持赞成态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点 A、B、C、D,根据下列语句画图:
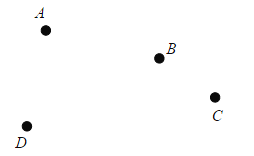
(1)画直线 AB;
(2)作射线 BC;
(3)画线段 CD;
(4)连接 DA 并延长,请使用直尺和圆规在线段 DA 的延长线上作线段 DE,使得 DE=2AD;
(5)数数看,此时图中共有 条线段,以 A 为端点的射线共有 条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.
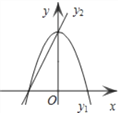
下列判断:
①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是![]() 或
或![]() .其中正确的个数是( )
.其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0.
![]()
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:|x+1|-|x-1|+2|x+5|(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南江县在“创国家级卫生城市”中,朝阳社区计划对某区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com