
【题目】把下列各数填在相应的大括号内:
0.275,﹣|﹣2|,﹣1.04,﹣(﹣10)2,﹣(﹣8), -![]() ,0,﹣
,0,﹣![]() .
.
负数集合{ …};
非负整数集合{ …};
整数集合{ …};
分数集合{ …}.
【答案】负数集合{﹣|﹣2|,﹣1.04,﹣(﹣10)2, -![]() ,
,![]() ,.…};
,.…};
非负整数集合{﹣(﹣8),0,…};
整数集合{﹣|﹣2|,﹣(﹣10)2,﹣(﹣8),0,…};
分数集合{0.275,﹣1.04,![]() ,…}.
,…}.
【解析】
负数是指比0小的数;非负整数是指不是负数的整数;整数包括正整数、负整数与0;有限小数与无线循环小数也属于分数;根据以上概念进行分类即可.
∵负数是指比0小的数,∴负数集合为{﹣|﹣2|,﹣1.04,﹣(﹣10)2, -![]() ,
,![]() ,.…};
,.…};
∵非负整数是指不是负数的整数,∴非负整数集合为{﹣(﹣8),0,…};
∵整数包括正整数、负整数与0,∴整数集合为{﹣|﹣2|,﹣(﹣10)2,﹣(﹣8),0,…};
∵有限小数与无线循环小数也属于分数,∴分数集合为{0.275,﹣1.04,![]() ,…}.
,…}.


科目:初中数学 来源: 题型:
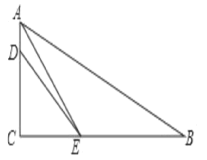
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求![]() 的值。.
的值。.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图. 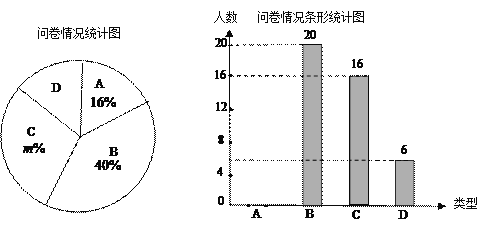
(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线AB经过点A(﹣2,0),与y轴的正半轴交于点B,且OA=2OB.
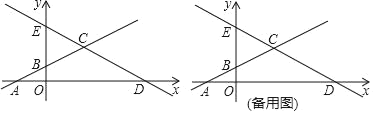
(1)求直线AB的函数表达式;
(2)点C在直线AB上,且BC=AB,点E是y轴上的动点,直线EC交x轴于点D,设点E的坐标为(0,m)(m>2),求点D的坐标(用含m的代数式表示);
(3)在(2)的条件下,若CE:CD=1:2,点F是直线AB上的动点,在直线AC上方的平面内是否存在一点G,使以C,G,F,E为顶点的四边形是菱形?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
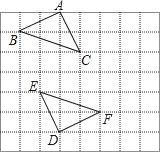
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC与△DEF关于点O成中心对称,△ABC与△DEF的顶点均在格点上.
(1)在图中直接画出O点的位置;
(2)若以O点为平面直角坐标系的原点,线段AD所在的直线为y轴,过点O垂直AD的直线为x轴,此时点B的坐标为(﹣2,2),请你在图上建立平面直角坐标系,并回答下面的问题:将△ABC先向右平移4个单位长度,再向下平移2个单位长度,得到△A1B1C1,请画出△A1B1C1,并直接写出点B1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
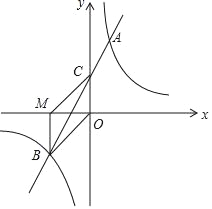
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”。图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速,设运动的时间为t秒,问:
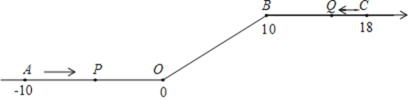
(1)动点P从点A运动至点C需要________秒;
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少?
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
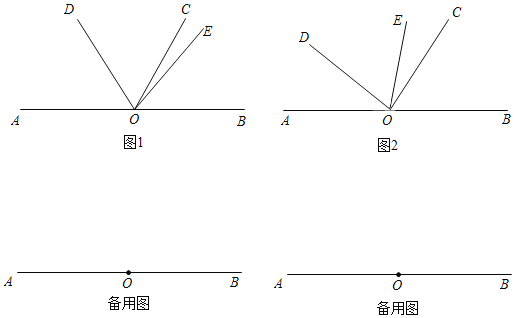
【题目】已知O为直线AB上一点,射线OD、OC、OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=α.
(1)如图1,α=70°,当OD平分∠AOC时,求∠EOB的度数.
(2)如图2,若∠DOC=2∠AOD,且α<80°,求∠EOB的度数(用含α的代数式表示);
(3)若α=90°,点F在射线OB上,若射线OF绕点O顺时针旋转n°(0<n<180),∠FOA=2∠AOD,OH平分∠EOC,当∠FOH=∠AOC时,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com