
【题目】已知,如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1.
(1)求证:△ABD∽△CBA;
(2)在原图上作DE∥AB交AC与点E,请直接写出另一个与△ABD相似的三角形,并求出DE的长.

科目:初中数学 来源: 题型:
【题目】燃放烟花爆竹是中国春节的传统民俗,可注重低碳、环保、健康的市民让今年的烟花爆竹遇冷.在江北区北滨路一烟花爆竹销售点了解到,某种品牌的烟花2013年除夕每箱进价100元,售价250元,销售量40箱 .而2014年除夕当天和去年当天相比,该店的销售量下降了![]() %(
%(![]() 为正整数),每箱售价提高了
为正整数),每箱售价提高了![]() %,成本增加了50%,其销售利润仅为去年当天利润的50%.则
%,成本增加了50%,其销售利润仅为去年当天利润的50%.则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
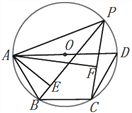
【题目】如图:点P是四边形ABCD外接圆⊙O上的任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD,连接PA,PB,PC,若PA= ![]() ,求点A到PB和PC的距离之和AE+AF是多少?
,求点A到PB和PC的距离之和AE+AF是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为( )

A.6 B.12 C.2![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=8cm,BC=16cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
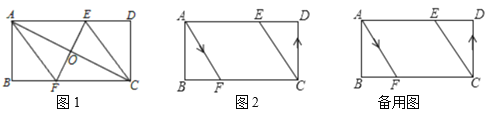
(1)如图1,连接AF、CE,判断四边形AFCE的形状,并说明理由;
(2)如图2,动点P、Q分别从A、C两点同时出发,P点沿着A→F→B→A匀速运动,Q点沿着C→D→E→C匀速运动,在运动过程中:
① 已知点P的速度为10cm/s,点Q的速度为8cm/s,运动时间为t秒,问当t为何值时,点A,C,P,Q组成的四边形为平行四边形?
② 点P,Q的运动路程分别为a,b(单位:cm,ab≠0),问当a,b满足怎样的关系式时,点A,C,P,Q组成的四边形为平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个等腰直角三角形△ABC和△CDE中,∠ACB=∠DCE=90°,AB=13![]() ,CD=5
,CD=5![]() ,△CDE绕点C在平面内自由旋转,当A、E、D三点共线时,AD的长是______.
,△CDE绕点C在平面内自由旋转,当A、E、D三点共线时,AD的长是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com