
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() 将
将![]() 绕点
绕点![]() .按顺时针方向旋转
.按顺时针方向旋转![]() 得
得![]() , 连接
, 连接![]() .
.
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时, 试判断
时, 试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

【答案】(1)见解析;(2)![]() 是直角三角形,理由见解析;(3)当
是直角三角形,理由见解析;(3)当![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
【解析】
(1)根据旋转的性质得到![]() ,再根据旋转角的度数得到∠OCD的度数,根据等边三角形的判定方法,即可证明.
,再根据旋转角的度数得到∠OCD的度数,根据等边三角形的判定方法,即可证明.
(2)根据旋转前后对应的两个三角形全等可得△BOC≌△ADC,利用全等三角形的性质得到∠ADC=∠BOC=![]() ,再利用△COD是等边三角形得∠ODC=60°,于是可计算出∠ADO的度数,再结合周角为360°,求出∠AOD的度数,探究是否存在等腰直角三角形的情况,进而判断△AOD的形状;
,再利用△COD是等边三角形得∠ODC=60°,于是可计算出∠ADO的度数,再结合周角为360°,求出∠AOD的度数,探究是否存在等腰直角三角形的情况,进而判断△AOD的形状;
(3)需要分三种情况讨论,即①要使AO=AD,需∠AOD=∠ADO;②要使OA=OD,需∠OAD=∠ADO;③要使OD=AD,需∠OAD=∠AOD;如对于①,∠AOD=190°-![]() ,∠ADO=
,∠ADO=![]() -60°,再结合∠AOD=∠ADO建立
-60°,再结合∠AOD=∠ADO建立![]() 的方程,求出
的方程,求出![]() 的度数,同理可以计算其他两种情况.
的度数,同理可以计算其他两种情况.
(1)证明:由旋转的性质得:![]() ,
,
![]()
![]() 是等边三角形;
是等边三角形;
(2)当![]() ,即
,即![]() °时,
°时,
![]() 是直角三角形.理由如下:
是直角三角形.理由如下:
由旋转的性质得:![]()
![]()
又是![]() 等边三角形,
等边三角形,
![]()
![]()
即![]() 是直角三角形;
是直角三角形;
(3)分三种情况:
①![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]() ;
;
②![]() 时,
时,![]()
![]()
![]()
![]()
![]() ;
;
③![]() 时,
时,![]()
![]()
![]() .
.
综上所述:当![]() 的度数为
的度数为![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图四边形ABCD是菱形,且∠ABC=60,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为2![]() 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.

A. ①②③ B. ②④⑤ C. ①②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, ![]() ,
, ![]() 与
与![]() 成正比例,
成正比例, ![]() 与
与![]() 成反比例,并且当
成反比例,并且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
(![]() )求
)求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(![]() )当
)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,
, ![]() .
.
【解析】分析:(1)首先根据![]() 与x成正比例,
与x成正比例, ![]() 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出![]() 和
和![]() 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
本题解析:
(![]() )设
)设![]() ,
, ![]() ,
,
则![]() ,
,
∵当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴
解得, ![]() ,
,
∴![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() .
.
(![]() )把
)把![]() 代入
代入![]() 得,
得,
![]() ,
,
解得: ![]() ,
, ![]() .
.
点睛:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=kx(k为常数,k≠0);(2)把已知条件(自变量与对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.
【题型】解答题
【结束】
24
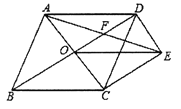
【题目】如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若菱形![]() 的边长为2,
的边长为2, ![]() .求
.求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成下列各题:平面内的两条直线有相交和平行两种位置关系。


(1)如图1,若![]() ,点P在AB,CD之间,求证:∠BPD=∠B+∠D;
,点P在AB,CD之间,求证:∠BPD=∠B+∠D;
(2)在图1中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图2,请写出![]() ,∠B,
,∠B,![]() ,
,![]() 之间的数量关系并说明理由;
之间的数量关系并说明理由;
(3)利用(2)的结论,求图3中![]() +∠G=n×90°,则n=____.
+∠G=n×90°,则n=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,增强居民环保意识,某校积极参加即将到来的6月5日的“世界环境日”宣传活动,七年级(1)班所有同学在同一天调查了各自家庭丢弃塑料袋的情况,统计结果的条形统计图如下:
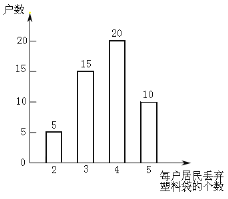
根据统计图,请回答下列问题:
(1)这组数据共调查了居民有多少户?
(2)这组数据的居民丢弃塑料袋个数的中位数是_______个,众数是 _______个.
(3)该校所在的居民区约有3000户居民,估计该居民区每天丢弃的塑料袋总数大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
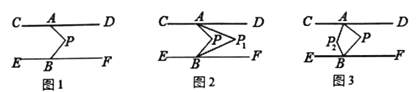
【题目】如图1,已知直线CD//EF ,点A、B分别在直线CD与EF上。P为两平行线间一点
(1)若∠DAP= 40° , ∠FBP=70°,求∠APB的度数是多少?
(2)直接写出∠DAP, ∠FBP, ∠APB之间有什么关系?
(3)利用(2)的结论解答:
①如图2, AP1、BP1,分别平分∠DAP,∠FBP,请你写出∠P与∠P1,的数量关系,并说明理由;
②如图3, AP2、 BP2分别平分∠CAP,∠EBP,若∠APB=β,求∠AP2B (用含β的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
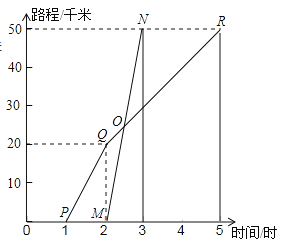
【题目】如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S和时间t的关系.象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发后多长时间追上甲?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com