
分析 根据题中直线平移的规律解决问题1、2、3;类似直线的平移规律,反比例函数图象的平移有相似的规律,则可解决问题4;先解方程组$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=x}\end{array}\right.$得M点坐标,然后利用两函数的图象的位置关系求不等式$\frac{4}{x}$>x的解集,则可解决问题5;先把不等式变形得到$\frac{4}{x-2}$>x-2,则可把问题5中的两函数图象向右平移2个单位得到y=$\frac{4}{x-2}$和y=x-2的图象,则把问题5中M点向右平移2个单位,则可确定图象y=$\frac{4}{x-2}$和图象y=x-2的交点坐标,然后利用两函数的图象的位置关系求不等式的解集,于是可解决问题6;由于不等式的解集为x<-1或1<x<3,则直线x=1为图象y=$\frac{8}{x-a}$的对称轴,所以y=$\frac{8}{x}$与y=2x的图象向右平移1个单位得到y=$\frac{8}{x-a}$和y=2x-b的图象,则利用平移的规律易得a和b的值,从而解决问题7;先根据点平移的规律,求出y=$\frac{2}{2x-1}$+3的图象向左平移1个单位,向下平移3个单位的解析式即可解决问题8.
解答 解:问题1:将直线y=$\frac{1}{2}$x-1向右平移2个单位,则其解析式为y=$\frac{1}{2}$(x-2)-1,即y=$\frac{1}{2}$x-2;
问题2:将直线y=$\frac{1}{3}$x+2向下平移1个单位,再向左平移3个单位,其解析式为y=$\frac{1}{3}$(x+3)+2-1,即y=$\frac{1}{3}$x+2;
问题3:由于将直线y=ax+a+1通过向下平移(a+2)个单位可以得到直线y=ax-1;
知识应用:
问题4:反比例函数y=$\frac{6}{x}$向右平移1个单位,其解析式为 y=$\frac{6}{x-1}$;
问题5:解方程组$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=x}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-2}\end{array}\right.$,所以反比例函数y1=$\frac{4}{x}$与正比例函数y2=x的交点M的坐标为(2,2)、(-2,-2);不等式$\frac{4}{x}$>x的解集为x<-2或0<x<2;
问题6:不等式$\frac{4}{x-2}$+1>x-1,即$\frac{4}{x-2}$>x-2,即把反比例函数y1=$\frac{4}{x}$与正比例函数y2=x的交点M的坐标为(2,2)、(-2,-2)向右平移2个单位,所以不等式$\frac{4}{x-2}$+1>x-1的解集为 x<0或2<x<4;
问题7:不等式$\frac{8}{x-a}$+b>2x变形为$\frac{8}{x-a}$>2x-b,由于不等式的解集为x<-1或1<x<3,则y=$\frac{8}{x}$与y=2x的图象向右平移一个单位得到y=$\frac{8}{x-a}$和y=2x-b的图象,所以a=1,b=2;问题8:点(x0,y0)向左平移1个单位,向下平移3个单位得到点(x0+1,y0-3),则把y=$\frac{2}{2x-1}$+3的图象向左平移1个单位,向下平移3个单位,其解析式为y=$\frac{2}{2(x-1)-1}$+3-2,即y=$\frac{2}{2x-3}$,故选C.
故答案为y=$\frac{1}{2}$x-2;y=$\frac{1}{3}$x+2;a+2;y=$\frac{6}{x-1}$;(2,2)、(-2,-2),x<-2或0<x<2;x<0或2<x<4;1,2;C.
点评 本题考查了反比例函数的综合题:熟练掌握反比例函数图象上点的坐标特征;运用一次函数图象的平移规律理解反比例函数图象的平移规律;会利用图象法解不等式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
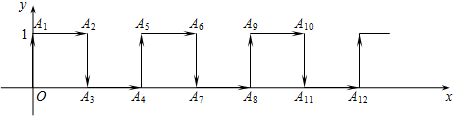
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
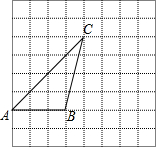 如图,△ABC的顶点A,B,C都在格点上,根据要求完成下列任务:
如图,△ABC的顶点A,B,C都在格点上,根据要求完成下列任务:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
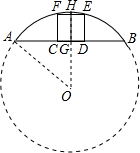 如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.
如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
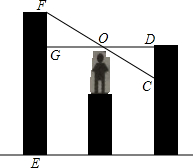 如图,某建筑公司想测出一电视塔EF的高度,身高为1.71m的公司员工登上10m高的顶楼阳台,他固定自己的站立位置,看到该电视塔的最高点时测出视线的仰角,再转过一个角度,用同样的大小的角度作为俯角,使视线刚好落在该员工的距离等于他与电视塔的距离的另一个建筑物的某一点C上,然后测出与该员工在同一水平线上的另一建筑物上的点D到点C的距离CD,就可以利用该距离求出该电视塔的高度,你能将其表示出来吗?
如图,某建筑公司想测出一电视塔EF的高度,身高为1.71m的公司员工登上10m高的顶楼阳台,他固定自己的站立位置,看到该电视塔的最高点时测出视线的仰角,再转过一个角度,用同样的大小的角度作为俯角,使视线刚好落在该员工的距离等于他与电视塔的距离的另一个建筑物的某一点C上,然后测出与该员工在同一水平线上的另一建筑物上的点D到点C的距离CD,就可以利用该距离求出该电视塔的高度,你能将其表示出来吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com