
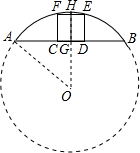
 如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.
如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2.分析 (1)先根据垂径定理求出AG的长,设OA=r,则OG=r-2,在Rt△AOG中根据勾股定理求出r的值即可;
(2)连接OF,设正方形CDEF的边长为a,EF交OH于点K,在Rt△OFK中根据勾股定理求出a的值即可.
解答 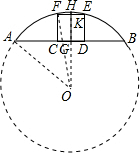 解:(1)∵AB=8,HG=2,
解:(1)∵AB=8,HG=2,
∴AG=4.
设OA=r,则OG=r-2,在Rt△AOG中,
∵AG2+OG2=OA2,即42+(r-2)2=r2,解得r=5,
∴弓形所在圆的半径长为5;
(2)连接OF,设正方形CDEF的边长为a,EF交OH于点K,
在Rt△OFK中,
∵OF2=FK2+OK2,
∴52=($\frac{a}{2}$)2+(3+a)2,解得a=8$\sqrt{29}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
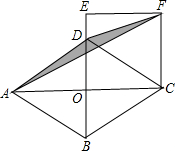 如图,在菱形ABCD中,对角线AC,BD长分别为8和6,延长OD到E,使OE=OC,以OE为边构造正方形OEFC,连接DF,AF,则△ADF的面积是( )
如图,在菱形ABCD中,对角线AC,BD长分别为8和6,延长OD到E,使OE=OC,以OE为边构造正方形OEFC,连接DF,AF,则△ADF的面积是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
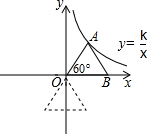 已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.
已知点A在双曲线y=$\frac{k}{x}$上,∠AOB=60°,AB=6,△AOB绕点O顺时针旋转120°后,点B刚好在双曲线上,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
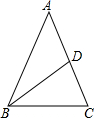 在等腰△ABC中,腰AB=AC,BD是AC边上的中线,已知△ABD的周长比△BCD的周长大8cm,且腰长是底边长的3倍,你能求出△ABC的周长吗?
在等腰△ABC中,腰AB=AC,BD是AC边上的中线,已知△ABD的周长比△BCD的周长大8cm,且腰长是底边长的3倍,你能求出△ABC的周长吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
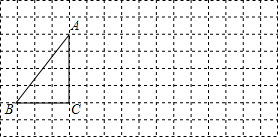 将下列方格纸中的△ABC向右平移8格,得到△A1B1C1.
将下列方格纸中的△ABC向右平移8格,得到△A1B1C1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com