
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
![]()
(1)写出数轴上点B表示的数 ;
(2)|5-3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如![]() 的几何意义是数轴上表示有理数
的几何意义是数轴上表示有理数![]() 的点与表示有理数3的点之间的距离.试探索:
的点与表示有理数3的点之间的距离.试探索:
①:若![]() ,则
,则![]() = .②:
= .②:![]() 的最小值为 .
的最小值为 .
(3)动点P从O点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为(>0)秒.
①:当=1时,A,P两点之间的距离为 ;②:当= 时,A,P之间的距离为2.
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒4个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.当t= ,P,Q之间的距离为4.
【答案】(1)![]() ;(2)①6或10;②20;(3)①6,②3或5;④2或4.
;(2)①6或10;②20;(3)①6,②3或5;④2或4.
【解析】
(1)根据两点间的距离公式可得数轴上点B表示的数;
(2)①根据绝对值的性质即可求解;
②根据两点间的距离公式即可求解;
(3)设经过t秒时,A,P之间的距离为2,根据距离的等量关系即可求解;
(4)设经过t秒时,P,Q之间的距离为4,根据距离的等量关系即可求解.
解:(1)点B表示的数8-20=-12.
故答案为:-12;
(2)①|x-8|=2,
x-8=±2,
则x=6或10.
故答案为:6或10;
②|x+12|+|x-8|的最小值为8-(-12)=20.
故答案为:20;
(3)设经过t秒时,A,P之间的距离为2.此时P点表示的数是5t,
则|8-5t|=2,
解得t=2或t= ![]() .
.
故当t为2或![]() 秒时,A,P两点之间的距离为2;
秒时,A,P两点之间的距离为2;
(4)设经过t秒时,P,Q之间的距离为4.
此时P点表示的数是5t,Q点表示的数-12+10t,
则|-12+10t-5t|=4
解得t=![]() 或t=
或t= ![]() .
.
故当t为![]() 或
或![]() 秒时,P,Q之间的距离为4.
秒时,P,Q之间的距离为4.


科目:初中数学 来源: 题型:
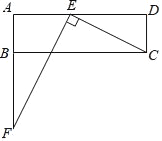
【题目】如图,在矩形ABCD中,已知 AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=4,AE=6,AD=14,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们自从有了用字母表示数,发现表达有关的数和数量关系更加简洁明了,从而更助于我们发现更多有趣的结论,请你按要求试一试。
(1)用代数式表示:
①![]() 与
与![]() 的差的平方;②
的差的平方;②![]() 、
、![]() 两数的平方和与
两数的平方和与![]() ,
,![]() 两数积的2倍的差;
两数积的2倍的差;
(2)当![]() =3,
=3,![]() =-2时,求第(1)题中①②所列的代数式的值;
=-2时,求第(1)题中①②所列的代数式的值;
(3)由第(2)题的结果,你发现了什么等式?
(4)利用你发现的结论:求20182-2×2018×2017+20172的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的统计图反映了我国2013年到2017年国内生产总值情况.(以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》)根据统计图提供的信息,下列推断不合理的是( )
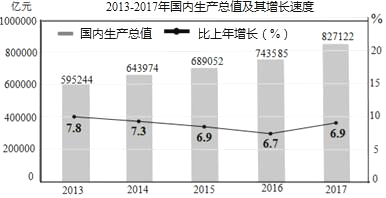
A. 与2016年相比,2017年我国国内生产总值有所增长
B. 2013﹣2016年,我国国内生产总值的增长率逐年降低
C. 2013﹣2017年,我国国内生产总值的平均增长率约为6.7%
D. 2016﹣2017年比2014﹣2015年我国国内生产总值增长的多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张长 9cm,宽 5cm 的长方形硬纸板,如图在长方形硬纸板的四个角上各截去一个边长为 0.5cm 的正方形,如图①所示,然后把它折叠成一个无盖的长方体小盒,如图②所示.

请问:
(1)折叠成一个无盖的长方体小盒的地面长.宽分别是多少?
(2)这个硬纸板折叠成的小盒容积是多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, OABC 的顶点 O、A、C 的坐标分别是(0,0),(2,0),(0.5,1),则点 B 的坐 标是( )
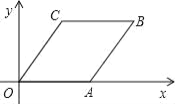
A.(1,2)B.(0.5,2)C.(2.5,1)D.(2,0.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
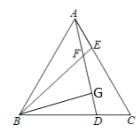
【题目】如图,△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F,BG⊥AD,垂足为G.
(1)求证:AD=BE;
(2)求∠AFB的度数;
(3)线段FG与BF有什么数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
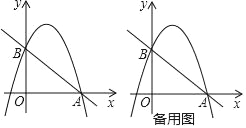
【题目】已知:如图,抛物线y=﹣x2+bx+C经过点B(0,3)和点A(3,0)
(1)求该抛物线的函数表达式和直线AB的函数表达式;
(2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com