练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】有一张长 9cm，宽 5cm 的长方形硬纸板，如图在长方形硬纸板的四个角上各截去一个边长为 0.5cm 的正方形，如图①所示，然后把它折叠成一个无盖的长方体小盒，如图②所示.

    请问：

    （1）折叠成一个无盖的长方体小盒的地面长.宽分别是多少？

    （2）这个硬纸板折叠成的小盒容积是多大？

    【答案】（1）8，4；（2）16

    【解析】

    （1）首先根据题意，用长方形硬纸板的长减去小正方形的边长的2倍，求出长方体纸盒的长是多少；然后用长方形硬纸板的宽减去小正方形的边长的2倍，求出长方体纸盒的宽是多少；（2）根据长方体的容积=长×宽×高，求出这个纸盒的容积是多少立方厘米即可．

    解：由题意得（1）无盖的长方体小盒的长=9-2×0.5=8

    无盖的长方体小盒的宽=5-2×0.5=4；

    （2）小盒的容积=8×4×0.5=16（立方厘米）
    故答案为：（1）8，4；（2）16．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则周长的最小值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着改革开放进程的推进，改变的不仅仅是人们的购物模式，就连支付方式也在时代的浪潮中发生着天翻地覆的改变，除了现金、银行卡支付以外，还有微信、支付宝以及其他支付方式．在一次购物中，小明和小亮都想从微信、支付宝、银行卡三种支付方式中选一种方式进行支付，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】公元3世纪初，我国学家赵爽证明勾定理的图形称为“弦图”．1876年美国总统Garfeild用图1（点C、点B、点C′三点共线）进行了勾股定理的证明．△ACB与△BC′B′是一样的直角三角板，两直角边长为a，b，斜边是c．请用此图1证明勾股定理．

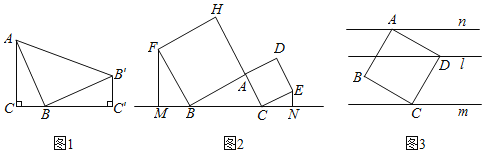
    拓展应用l：如图2，以△ABC的边AB和边AC为边长分别向外做正方形ABFH和正方形ACED，过点F、E分别作BC的垂线段FM、EN，则FM、EN、BC的数量关系是怎样？直接写出结论　 　．

    拓展应用2：如图3，在两平行线m、n之间有一正方形ABCD，已知点A和点C分别在直线m、n上，过点D作直线l∥n∥m，已知l、n之间距离为1，l、m之间距离为2．则正方形的面积是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=20，

    （1）写出数轴上点B表示的数 ；

    （2）|5－3|表示5与3之差的绝对值，实际上也可理解为5与3两数在数轴上所对的两点之间的距离．如的几何意义是数轴上表示有理数的点与表示有理数3的点之间的距离．试探索：

    ①：若，则 = .②：的最小值为 .

    （3）动点P从O点出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动时间为（＞0）秒．

    ①：当=1时，A，P两点之间的距离为 ；②：当= 时，A，P之间的距离为2.

    （4）动点P，Q分别从O，B两点，同时出发，点P以每秒4个单位长度沿数轴向右匀速运动，Q点以P点速度的两倍，沿数轴向右匀速运动，设运动时间为t（t＞0）秒．当t= ，P，Q之间的距离为4.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

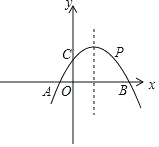
    【题目】如图，已知抛物线y＝ax2+bx+1与x轴分别交于A(﹣1，0)，B(3，0)，与y轴交于点C．

    (1)求抛物线解析式；

    (2)在直线BC上方的抛物线上有点P，使△PBC面积为1，求出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】红星中学九年级(1)班三位教师决定带领本班名学生利用假期去某地旅游，枫江旅行社的收费标准为：教师全价，学生半价；而东方旅行社不管教师还是学生一律八折优惠，这两家旅行社的全价都是500元。

    (1)用含的式子表示三位教师和位学生参加这两家旅行社所需的费用各是多少元；

    (2)如果=50时，请你计算选择哪一家旅行社较为合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A（4，0）及在第一象限的动点P（x，y），且x+y=5，0为坐标原点，设△OPA的面积为S．

    （1）求S关于x的函数表达式；

    （2）求x的取值范围；

    （3）当S=4时，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

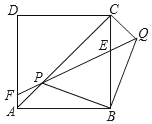
    【题目】如图，正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上（点P与A、C不重合），QP与BC交于E，QP延长线与AD交于点F，连接CQ．

    （1）①求证：AP=CQ；②求证：PA2=AFAD；

    （2）若AP：PC=1：3，求tan∠CBQ．

    查看答案和解析>>

    同步练习册答案