练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

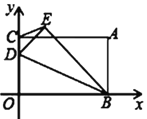
    【题目】如图，将一矩形OABC放在平面直角坐标系中，O为原点，点B、C分别在x轴、y轴上，点A（4，3），点D为线段OC上一动点，将△BOD沿BD翻折，点O落在点E处，连接CE，则CE的最小值为______．

    【答案】1

    【解析】

    如图，由三角形三边关系可得点C、E、B在一条直线上时CE值最小，根据矩形性质及点A坐标可得OB、OC的长，利用勾股定理可求出BC的长，折叠性质可得BE=OB， 根据线段的和差关系即可得答案．

    如图，连接BC，

    ∵将△BOD沿BD翻折，点O落在点E处，

    ∴BE=OB，

    ∵CE+BE≥BC，

    ∴点C、E、B在一条直线上时CE值最小，

    ∵点A（4，3），点B、C分别在x轴、y轴上，

    ∴OB=4，OC=3，

    ∴BC==5，

    ∴CE=BC-BE=BC-OB=1，

    故答案为：1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知在平行四边形中，点为边上一点，过点作于点，

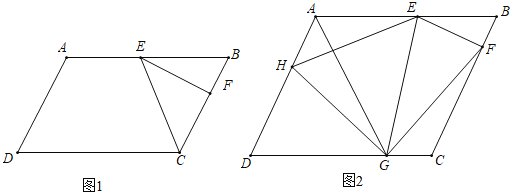
    （1）如图1，连接，若点为中点，，，，求的长．

    （2）如图2，作的平分线交于点，连接，若，为等边三角形，且，，求证：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

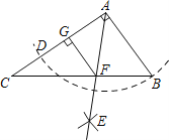
    【题目】如图，在Rt△ABC中，∠BAC=90°，AB=1，tanC=，以点A为圆心，AB长为半径作弧交AC于D，分别以B、D为圆心，以大于BD长为半径作弧，两弧交于点E，射线AE与BC于F，过点F作FG⊥AC于G，则FG的长为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

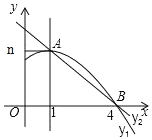
    【题目】如图，是抛物线y1=ax2+bx+c（a≠0）的图象的一部分，抛物线的顶点坐标是A（1，n），与x轴的一个交点B（4，0），直线y2=mx+d（m≠0）与抛物线交于A，B两点，下列结论：

    ①3a+b=0，②方程ax2+bx+c+1=n有两个相等的实数根，③b2=4a（c﹣n），④当1＜x＜4时，有y2＞y1，⑤ax2+bx≤a+b，其中正确的结论是____（只填写序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A（1，0），已知抛物线y=x2+mx﹣2m（m是常数），顶点为P．

    （1）当抛物线经过点A时．

    ①求顶点P的坐标；

    ②设直线l：y=3x+1与抛物线交于B、C两点，抛物线上的点M的横坐标为n（﹣1≤n≤3），过点M作x轴的垂线，与直线l交于点Q，若MQ=d，当d随n的增大而减少时，求n的取值范围．

    （2）无论m取何值，该抛物线都经过定点H，当∠AHP=45°时，求抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

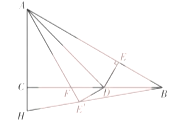
    【题目】如图，在中，，，是边上一动点，过点作于点．连接，与关于所在的直线对称，且所在的直线与直线相交于点，直线与直线相交于点．若点到的斜边和一条直角边的距离恰好相等，则的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线与轴交于点和点，与直线交于点和点，为抛物线的顶点，直线是抛物线的对称轴．

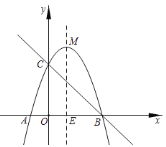
    （1）求抛物线的解析式及点的坐标．

    （2）点为直线上方抛物线上一点，设为点到直线的距离，当有最大值时，求点的坐标．

    （3）若点为直线上一点，作点关于轴的对称点，连接，，当是直角三角形时，直接写出点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，等边的边在轴上，点，点，点在第一象限．

    （1）若抛物线经过点、、，求抛物线的表达式．

    （2）点是平面内一点，以点、、、为顶点的四边形是平行四边形，现将抛物线平移得到抛物线，若抛物线经过、两点，求抛物线的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在菱形ABCD中，∠BAD＝60°

    (1) 如图1，点E为线段AB的中点，连接DE、CE．若AB＝4，求线段EC的长

    (2) 如图2，M为线段AC上一点（不与A、C重合），以AM为边向上构造等边三角形AMN，线段MN与AD交于点G，连接NC、DM，Q为线段NC的中点，连接DQ、MQ，判断DM与DQ的数量关系，并证明你的结论

    (3) 在(2)的条件下，若AC＝，请你直接写出DM＋CN的最小值

    查看答案和解析>>

    同步练习册答案