
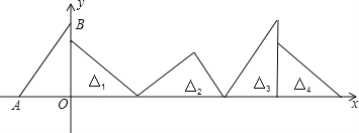
【题目】 如图,在直角坐标系中,已知点A(-3,0),B(0,4),AB=5,对△OAB连续做旋转变换,依次得到△1,△2,△3,△4,…,则△2017的直角顶点的坐标为______.
【答案】(8064,0)
【解析】
得到△ABC的周长为12,根据旋转变换可得△OAB的旋转变换为每3次一个循环,由于2017÷3=672…1,于是可判断三角形2017与三角形1的状态一样,然后计算672×12即可得到三角形2017的直角顶点坐标.
解:∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∵AB=5,
∴△ABC的周长=3+4+5=12,
∵△OAB每连续3次后与原来的状态一样,
∵2017÷3=672…1,
∴△2017的直角顶点是第672个循环组后第一个三角形的直角顶点,
∴三角形2017的直角顶点的横坐标=672×12=8064,
∴三角形2017的直角顶点坐标为(8064,0),
故答案为:(8064,0).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上的动点(不与
上的动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]()
于点![]() .以
.以![]() 为直径作
为直径作![]() ,并在
,并在![]() 内作内接矩形
内作内接矩形![]() ,令
,令![]() .
.
![]() 用含
用含![]() 的代数式表示
的代数式表示![]() 的面积
的面积![]() ;
;
![]() 当
当![]() 为何值时,
为何值时,![]() 与直线
与直线![]() 相切?
相切?
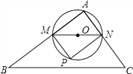
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
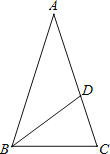
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约生活用水,计划制定每位居民统一的月用水量标准,然后根据标准,实行分段收费.为此,对居民上年度的月均用水量进行了抽样调查,并根据调查结果绘制了上年度月均用水量的频数分布直方图(图中分组含最低值,不含最高值),请根据图中信息解答下列问题:
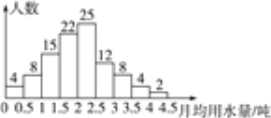
(1)本次调查的居民人数为__________人;
(2)本次调查的居民月均用水量的中位数落在频数分布直方图中的第__________小组内(从左至右数);
(3)当地政府希望让85%左右居民的月均用水量低于制定的月用水量标准,根据上述调查结果,你认为月用水量标准(取整数)定为多少吨时较为合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果两个一次函数的一次项系数和常数项互换,即y=kx+b和y=bx+k(其中|k|≠|b|),称这样的两个一次函数为互助一次函数,例如![]() 和
和![]() 就是互助一次函数.根据规定解答下列问题:
就是互助一次函数.根据规定解答下列问题:
(1)填空:一次函数![]() 与它的互助一次函数的交点坐标为______
与它的互助一次函数的交点坐标为______
(2)若两个一次函数y=(k-b)x – k - 2b与![]() 是互助一次函数,求两函数图象与y轴围成的三角形的面积.
是互助一次函数,求两函数图象与y轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:![]() 分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:
分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:![]() 经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
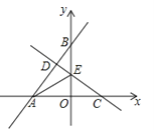
(1)当点C的坐标为![]() 时,①求直线l2的函数表达式;②求证:AE平分
时,①求直线l2的函数表达式;②求证:AE平分![]() ;
;
(2)问:是否存在点C,使![]() 是以CE为一腰的等腰三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
是以CE为一腰的等腰三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
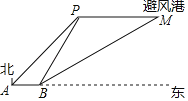
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,∠A=35°,∠C=40°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com