
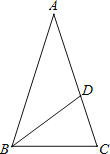
【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由等腰三角形ABC中,顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;
(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;
(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.
试题解析:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∵∠CBD=∠A=36°,∠C=∠C,
∴△ABC∽△BCD;
(2)∵∠A=∠ABD=36°,
∴AD=BD,
∵BD=BC,
∴AD=BD=CD=1,
设CD=x,则有AB=AC=x+1,
∵△ABC∽△BCD,
∴![]() ,即
,即![]() ,
,
整理得:x2+x-1=0,
解得:x1=![]() ,x2=
,x2=![]() (负值,舍去),
(负值,舍去),
则x=![]() ;
;
(3)过B作BE⊥AC,交AC于点E,
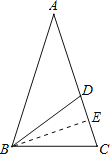
∵BD=CD,
∴E为CD中点,即DE=CE=![]() ,
,
在Rt△ABE中,cosA=cos36°=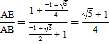 ,
,
在Rt△BCE中,cosC=cos72°=![]() ,
,
则cos36°-cos72°=![]() -
-![]() =
=![]() .
.


科目:初中数学 来源: 题型:
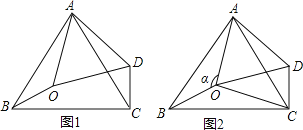
【题目】如图1,在△ABC中,∠BAC=60°,点0是△ABC内一点,△AB0![]() △ACD,连接OD.
△ACD,连接OD.
(1)求证△AOD为等边三角形。
(2)如图2,连接OC,若∠BOC=130°,∠AOB=![]() .
.
①求∠OCD的度数
②当△OCD是等腰三角形时,求∠![]() 的度数
的度数
 、
、
查看答案和解析>>
科目:初中数学 来源: 题型:
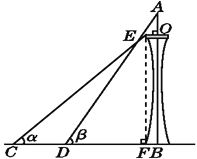
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
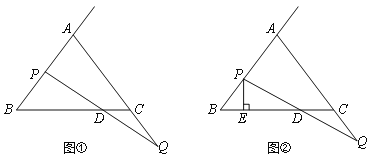
【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
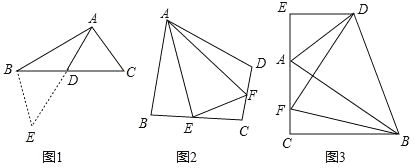
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
问题拓展:
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=![]() AF.
AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
科目:初中数学 来源: 题型:
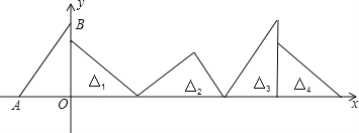
【题目】 如图,在直角坐标系中,已知点A(-3,0),B(0,4),AB=5,对△OAB连续做旋转变换,依次得到△1,△2,△3,△4,…,则△2017的直角顶点的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是__cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com