
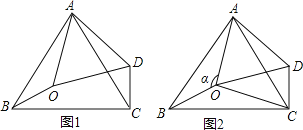
【题目】如图1,在△ABC中,∠BAC=60°,点0是△ABC内一点,△AB0![]() △ACD,连接OD.
△ACD,连接OD.
(1)求证△AOD为等边三角形。
(2)如图2,连接OC,若∠BOC=130°,∠AOB=![]() .
.
①求∠OCD的度数
②当△OCD是等腰三角形时,求∠![]() 的度数
的度数
 、
、
【答案】(1)见解析;.(2)①∠OCD=70°;②可以是130°,100°,115°.
【解析】
(1)根据全等三角形得到AO=AD,∠BAO=∠CAD,由∠BAC=60°,求得∠OAD=60°,即可得到结论;
(2)①根据△AOD为等边三角形,求得∠AOD=∠ADO=60°,求得∠DOC=360°-α-130°-60°=170°-α,根据全等三角形的性质得到∠ADC=∠AOB=α,于是得到∠OCD=180°-∠DOC-∠ODC=70°;②当△OCD是等腰三角形时,(Ⅰ)当OD=OC,由∠DOC=170°-α,得到∠OCD=∠ODC= ![]() α+5°,列方程得到α=130°(Ⅱ)当OD=CD,于是得到∠OCD=∠COD=170°-α;求得∠ODC=180°-2×170°+2α=2α-160°,列方程即可得到α=100°;(Ⅲ)当OC=CD,于是得到∠ODC=∠COD=170°-α,列方程即可得到α=115°.
α+5°,列方程得到α=130°(Ⅱ)当OD=CD,于是得到∠OCD=∠COD=170°-α;求得∠ODC=180°-2×170°+2α=2α-160°,列方程即可得到α=100°;(Ⅲ)当OC=CD,于是得到∠ODC=∠COD=170°-α,列方程即可得到α=115°.
(1)证明:∵△ABO≌△ACD
∴∠OAB=∠CAD
∴AO=AD
∴∠OAB+∠OAC=∠OAC+∠CAD=60°
△AOD为等边三角形.
(2)①∵△AOD为等边三角形,
∴∠AOD=∠ADO=60°,
∵∠BOC=130°,∠AOB=∠α,
∴∠DOC=360°α130°60°=170°α,
∵△ABO≌△ACD,
∴∠ADC=∠AOB=α,
∴∠ODC=α60°,
∴∠OCD=180°∠DOC∠ODC=70°;
②当△OCD是等腰三角形时,
(Ⅰ)当OD=OC,∵∠DOC=170°α,
∴∠OCD=∠ODC=![]() α+5°,
α+5°,
∴60°+![]() α+5°=α,
α+5°=α,
解得:α=130°
(Ⅱ)当OD=CD,∴∠OCD=∠COD=170°α;
∴∠ODC=180°2×170°+2α=2α160°,
∴60°+2α160°=α,
解得:α=100°;
(Ⅲ)当OC=CD,∴∠ODC=∠COD=170°α,
∴170°α+60°=α,
解得:α=115°.
综上所述:当△OCD是等腰三角形时,∠α的度数为:130°,100°,115°.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】用火柴棒按下图的方式搭塔式三角形,第一个图用了3根火柴棒,第二个图用了9根火柴棒,第三个图用了18根火柴棒,......,照这样下去,第9个图用了_____根火柴棒.
 ……
……
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形的纸片ABCD沿BD对折,使C点落在E点处,BE与AD相交于点O。
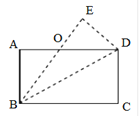
(1)由折叠可知△BCD≌△BED,除此之外,图中还存在其他的全等三角形,请写出其他一组全等三角形__________________.
(2)图中有等腰三角形吗?请你找出来__________________.
(3)若AB=6,BC=8,求OB的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,∠B=α,在AB,BC上分别找一点E,F,使△DEF的周长最小,此时,∠EDF=______。(用含α的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程.
如图:在四边形ABCD中, ![]() ,
, ![]() 于点D,
于点D, ![]() 于点F,求证:
于点F,求证: ![]()

证明: ![]() (已知)
(已知)
![]()
![]() AD// ( )
AD// ( )
![]() = ( )
= ( )
![]() ,
, ![]() (已知)
(已知)
![]() ( )
( )
![]() BD// ( )
BD// ( )
![]() = ( )
= ( )
![]()
![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)写出点A,B,C的坐标并画出三角形ABC;
(2)若将三角形ABC平移后得到三角形A1B1C1,平移后点C的对应点C1的坐标为(2,1),请画出三角形A1B1C1,并写出A1,B1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
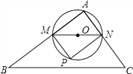
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上的动点(不与
上的动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]()
于点![]() .以
.以![]() 为直径作
为直径作![]() ,并在
,并在![]() 内作内接矩形
内作内接矩形![]() ,令
,令![]() .
.
![]() 用含
用含![]() 的代数式表示
的代数式表示![]() 的面积
的面积![]() ;
;
![]() 当
当![]() 为何值时,
为何值时,![]() 与直线
与直线![]() 相切?
相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
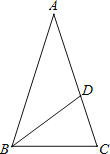
【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com