练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列方程中，为一元二次方程的是（ ）

    A. x＝2y－3 B. ＋1＝3 C. x2＋3x－1＝x2＋1 D. x2＝0

    【答案】D

    【解析】一元二次方程必须同时满足三个条件：

    是整式方程，即等号两边都是整式;方程中如果有分母,且未知数在分母，那么这个方程就是分式方程，不是一元二次方程;方程中如果有根号，且未知数在根号内，那么这个方程也不是一元二次方程（是无理方程）.

    ②只含有一个未知数；

    ③未知数项的最高次数是2.

    A. x＝2y－3,有两个未知数，故本选项不可选；

    B. ＋1＝3，分母有未知数，不是整式方程，故本选项不能选；

    C. x2＋3x－1＝x2＋1,方程化为3x－1＝1，不是二次方程，故不能选；

    D. x2＝0，符合条件，可以选..

    故选：D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】随着我国经济社会的发展，人民对于美好生活的追求越来越高．某社区为了了解家庭对于文化教育的消费悄况，随机抽取部分家庭，对每户家庭的文化教育年消费金额进行问卷调査，根据调查结果绘制成两幅不完整的统计图表．

    请你根据统计图表提供的信息，解答下列问题：

    组別

    家庭年文化教育消费金额x（元）

    户数

    A

    x≤5000

    36

    B

    5000＜x≤10000

    m

    C

    10000＜x≤15000

    27

    D

    15000＜x≤20000

    15

    E

    x＞20000

    30

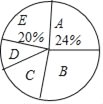
    （1）本次被调査的家庭有__________户，表中 m=__________；

    （2）本次调查数据的中位数出现在__________组．扇形统计图中，D组所在扇形的圆心角是__________度；

    （3）这个社区有2500户家庭，请你估计家庭年文化教育消费10000元以上的家庭有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，折线ABC是在某市乘出租车所付车费y（元）与行车里程x（km）之间的函数关系图象．

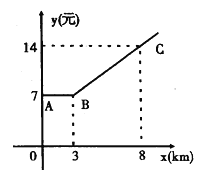
    （1）根据图象，求当x≥3时的函数关系式；

    （2）某人乘坐2.5km，应付多少钱？

    （3）某人乘坐13km，应付多少钱？

    （4）若某人付车费30.8元，出租车行驶了多少路程？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB=AC，∠A=36°，AC的垂直平分线MN交AB于D，AC于M，以下结论：

    ①△BCD是等腰三角形；②射线CD是∠ACB的角平分线；③△BCD的周长C△BCD=AB+BC；④△ADM≌△BCD。

    正确的有（ ）

    A. ①② B. ①③ C. ①②③ D. ③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，AB=AC，D是BC的中点，点E在AD上.

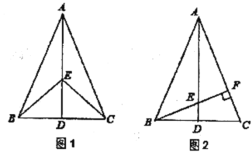
    （1）求证：BE=CE；

    （2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其他条件不变.求证：EF=CF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

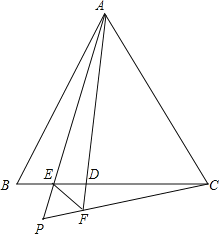
    【题目】如图，在△ABC中，点D为线段BC上一点（不含端点），AP平分∠BAD交BC于E，PC与AD的延长线交于点F，连接EF，且∠PEF＝∠AED．

    （1）求证：AB＝AF；

    （2）若△ABC是等边三角形．

    ①求∠APC的大小；

    ②想线AP，PF，PC之间满足怎样的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

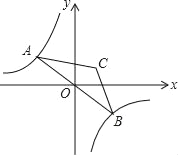
    【题目】如图，点A是双曲线y=﹣在第二象限分支上的一个动点，连接AO并延长交另一分支于点B，以AB为底作等腰△ABC，且∠ACB=120°，点C在第一象限，随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y=上运动，则k的值为（ ）

    A. 3 B. 4 C. 2.5 D. 7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

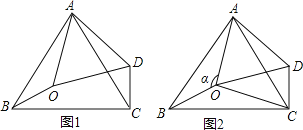
    【题目】如图1，在△ABC中，∠BAC=60°，点0是△ABC内一点，△AB0△ACD，连接OD.

    （1）求证△AOD为等边三角形。

    （2）如图2，连接OC，若∠BOC=130°，∠AOB=.

    ①求∠OCD的度数

    ②当△OCD是等腰三角形时，求∠的度数

    、

    查看答案和解析>>

    科目：初中数学 来源： 题型：

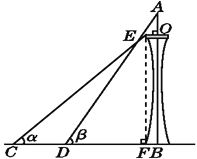
    【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)

    查看答案和解析>>

    同步练习册答案