
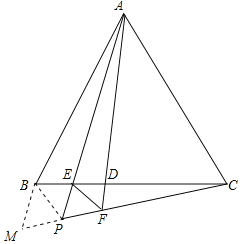
【题目】如图,在△ABC中,点D为线段BC上一点(不含端点),AP平分∠BAD交BC于E,PC与AD的延长线交于点F,连接EF,且∠PEF=∠AED.
(1)求证:AB=AF;
(2)若△ABC是等边三角形.
①求∠APC的大小;
②想线AP,PF,PC之间满足怎样的数量关系,并证明.
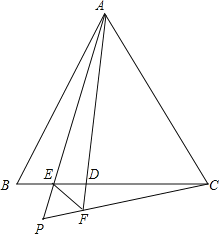
【答案】(1)详见解析;(2)①60°;②AP=PF+PC,理由详见解析.
【解析】
(1)由已知证出∠AEB=∠AEF,∠BAP=∠FAP,证明△AEB≌△AEF,即可得出AB=AF;
(2)①由等边三角形的性质得出AB=AC=BC,∠BAC=60°,证出AF=AC,设∠BAP=∠FAP=x,则∠FAC=60°﹣2x,求出∠AFC=x+60°,由三角形的外角性质得出∠AFC=∠FAP+∠APC=x+∠APC,即可得出结果;
②延长CP至点M,使PM=PF,连接BM、BP,先证明△APB≌△APF,得出∠APC=∠APB=60°,PB=PF,得出∠BPM=60°,PM=PB,得出△BPM是等边三角形,得出BP=BM,∠ABP=∠CBM=60°+∠PBC,再证明△ABP≌△CBM,即可得出结论.
(1)证明:∵∠PEF=∠AED,
∴180°﹣∠PEF=180°﹣∠AED,
∴∠AEB=∠AEF,
∵AP平分∠BAD,
∴∠BAP=∠FAP,
在△AEB和△AEF中,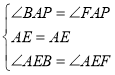 ,
,
∴△AEB≌△AEF(ASA),
∴AB=AF;
(2)解:①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
∵AB=AF,
∴AF=AC,
设∠BAP=∠FAP=x,则∠FAC=60°﹣2x,
在△ACF中,∠AFC=![]() [180°﹣(60°﹣2x)]=x+60°,
[180°﹣(60°﹣2x)]=x+60°,
又∵∠AFC=∠FAP+∠APC=x+∠APC,
∴∠APC=60°;
②AP=PF+PC,理由如下:
延长CP至点M,使PM=PF,连接BM、BP,如图所示:
在△APB和△APF中,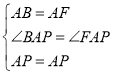 ,
,
∴△APB≌△APF(SAS),
∴∠APC=∠APB=60°,PB=PF,
∴∠BPM=60°,PM=PB,
∴△BPM是等边三角形,
∴BP=BM,∠ABP=∠CBM=60°+∠PBC,
在△ABP和△CBM中,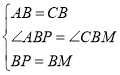 ,
,
∴△ABP≌△CBM(SAS),
∴AP=CM=PM+PC=PF+PC.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,每个小正方形的边长均为
,每个小正方形的边长均为![]() ,阴影部分是一个正方形.
,阴影部分是一个正方形.
(1)阴影部分的面积是__________,边长是____________;
(2)写出不大于阴影正方形边长的所有正整数;
(3)![]() 为阴影正方形边长的小数部分,
为阴影正方形边长的小数部分,![]() 为
为![]() 的整数部分,求
的整数部分,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
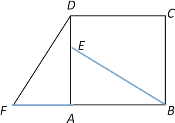
求:(1)指出旋转中心和旋转角度
(2)求DE的长度
(3)BE与DF的位置关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
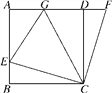
【题目】如图,在正方形ABCD中,E是AB边上一点,F是AD延长线上一点,BE=DF.
(1)求证:CE=CF;
(2)若点G在AD边上,且∠GCE=45°,BE=3,DG=5,求GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形的纸片ABCD沿BD对折,使C点落在E点处,BE与AD相交于点O。
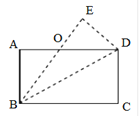
(1)由折叠可知△BCD≌△BED,除此之外,图中还存在其他的全等三角形,请写出其他一组全等三角形__________________.
(2)图中有等腰三角形吗?请你找出来__________________.
(3)若AB=6,BC=8,求OB的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程.
如图:在四边形ABCD中, ![]() ,
, ![]() 于点D,
于点D, ![]() 于点F,求证:
于点F,求证: ![]()

证明: ![]() (已知)
(已知)
![]()
![]() AD// ( )
AD// ( )
![]() = ( )
= ( )
![]() ,
, ![]() (已知)
(已知)
![]() ( )
( )
![]() BD// ( )
BD// ( )
![]() = ( )
= ( )
![]()
![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com