
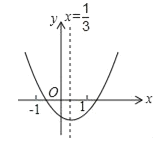
【题目】小华从二次函数y=ax2+bx+c的图象(如图)中观察得到了下面五条信息:
①abc>0 ②2a﹣3b=0 ③b2﹣4ac>0 ④a+b+c>0 ⑤4b<c
则其中结论正确的个数是( )
A.2个B.3个C.4个D.5个
【答案】B
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
①因为函数图象与y轴的交点在y轴的负半轴可知,c<0,
由函数图象开口向上可知,a>0,由①知,c<0,
由函数的对称轴在x的正半轴上可知,x=![]() >0,故b<0,故abc>0;故此选项正确;
>0,故b<0,故abc>0;故此选项正确;
②因为函数的对称轴为x=![]() =
=![]() ,故2a=3b,即2a+3b=0;故此选项错误;
,故2a=3b,即2a+3b=0;故此选项错误;
③因为图象和x轴有两个交点,所以b24ac>0,故此选项正确;
④把x=1代入y=ax2+bx+c得:a+b+c<0,故此选项错误;
⑤当x=2时,y=4a+2b+c=2×(3b)+2b+c=c4b,
而点(2,c4b)在第一象限,
∴⑤c4b>0,故此选项正确;
其中正确信息的有①③⑤,
故选:B.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验A考查的概率是 ;
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;
(3)他们三人都参加实验A考查的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽所在生活小区的管理人员为了方便业主合理规范摆放机动车,在小区内部道路的一侧按照标准画出了一些停车位.
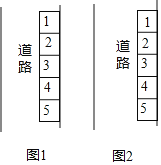
(1)如图1,小明家楼下的道路上有五个空停车位,标号分别为1,2,3,4,5,如果有一辆机动车要随机停在这五个停车位中的一个里边,则该机动车停在“标号是奇数”停车位的概率是 .
(2)如图2,小丽家楼下的道路上有四个空停车位,标号分别为1,2,3,4,如果有两辆机动车要随机停在这四个停车位中的两个里边,请用列表或画树状图的方法得出这两辆机动车停在“标号是一个奇数和一个偶数”停车位的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x与抛物线y=![]() x2交于A、B两点.
x2交于A、B两点.
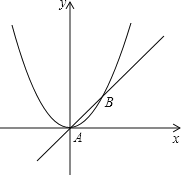
(1)求交点A、B的坐标;
(2)记一次函数y=x的函数值为y1,二次函数y=![]() x2的函数值为y2.若y1>y2,求x的取值范围.
x2的函数值为y2.若y1>y2,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
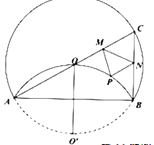
【题目】如图,将半径为4的![]() 沿弦
沿弦![]() 折叠,圆上点
折叠,圆上点![]() 折叠后恰好与圆点
折叠后恰好与圆点![]() 重合,连接
重合,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .点
.点![]() 为弧
为弧![]() 上一点,
上一点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一动点,则
上一动点,则![]() 周长的最小值为___________.
周长的最小值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察表格:根据表格解答下列问题:
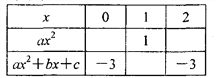
(l) a=______,b=_____,c=_____;
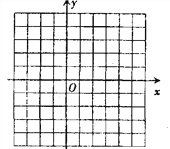
(2) 在右图的直角坐标系中画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c > -3成立;
(3)该图象与x轴两交点从左到右依次分别为A、B,与y轴交点为C,求过这三个点的外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
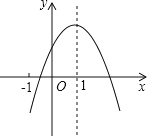
【题目】已知二次函数![]() 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论:
①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).
其中正确结论的序号有 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形
(1)如图1,在半对角四边形ABCD中,∠B=![]() ∠D,∠C=
∠D,∠C=![]() ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO,∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.求证:四边形DBCF是半对角四边形;
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G,当DH=BG=2时,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com