
分析 根据例题可以得到:方程的左边与右边的式子形式完全相同,只是左边是未知数,右边是把未知数换成了具体的数,则方程的解是方程右边的两部分,据此即可求解.
解答 解:(1)根据上面的规律,猜想关于x的方程$x+\frac{1}{x}$=$n+\frac{1}{n}$的解是 x1=n,x2=$\frac{1}{n}$;
故答案为:x1=n,x2=$\frac{1}{n}$.
(2)类似的,关于x的方程x-$\frac{1}{x}$=m-$\frac{1}{m}$的解是 x1=m,x2=-$\frac{1}{m}$;
(3)x+$\frac{1}{x-3}$=a+$\frac{1}{a-3}$,
可得:x-3+$\frac{1}{x-3}$=a-3+$\frac{1}{a-3}$,
可得:x1=a,x2=$\frac{1}{a-3}$+3=$\frac{3a-8}{a-3}$.
点评 本题考查分式方程的解,正确理解例题,发现方程与解之间的关系:方程的左边与右边的式子形式完全相同,只是左边是未知数,右边是把未知数换成了具体的数,则方程的解是方程右边的两部分,是解题的关键.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
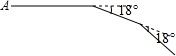 如图,小亮从A点出发前进10m,向右转18°,再前进10m,又向右转18°,…,这样一直走下去,他第一次回到出发点A时,一共走了200m.
如图,小亮从A点出发前进10m,向右转18°,再前进10m,又向右转18°,…,这样一直走下去,他第一次回到出发点A时,一共走了200m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com