
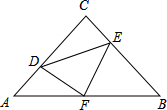
 如图,在等腰直角三角形ABC中,∠C=90°,AC=8,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则四边形CDFE的面积是
如图,在等腰直角三角形ABC中,∠C=90°,AC=8,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则四边形CDFE的面积是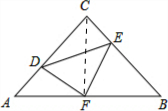
|
| 8 | ||
|
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
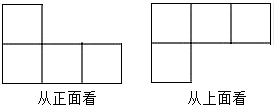 几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )
几何体的形状图如图所示.搭成这个几何体用到的小正方形的个数最多是( )| A、4个 | B、5个 | C、6个 | D、7个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.
如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.
某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.查看答案和解析>>
科目:初中数学 来源: 题型:
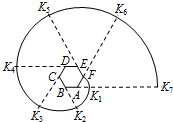 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com