
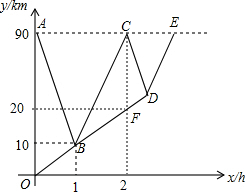
 某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.
某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.| 7 |
| 9 |
| 7 |
| 9 |
| 560 |
| 9 |
| 7 |
| 9 |
| 25 |
| 9 |
| 560 |
| 9 |
| 25 |
| 9 |


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
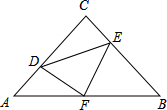 如图,在等腰直角三角形ABC中,∠C=90°,AC=8,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则四边形CDFE的面积是
如图,在等腰直角三角形ABC中,∠C=90°,AC=8,点F是AB的中点,点D、E分别在AC、BC边上运动,且始终保持DF⊥EF,则四边形CDFE的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
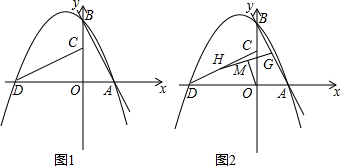
 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结论:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0,其中正确的结论是
已知二次函数y=ax2+bx+c的图象如图,其对称轴x=-1,给出下列结论:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0,其中正确的结论是查看答案和解析>>
科目:初中数学 来源: 题型:
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k1 |
| x |
| k2 |
| x |
| k3 |
| x |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com