
分析 (1)因为原方程有两个实数根,故判别式△=(m+n+2)2-8m=(m+n-2)2+8n≥0,且α+β=m+m+2,αβ=2m,即可得出结论;
(2)因为α≤β,故只需求(2-α)(2-β)≤0即可;
(3)先根据条件确定动点所在的边,再确定点的坐标.
解答 解:(1)∵α、β为方程x2-(m+n+)x+2m=0(n≥0)的两个实数根,
∴判别式△=(m+n+2)2-8m=(m+n-2)2+8n≥0,
且α+β=m+n+2,αβ=2m,
于是m=$\frac{1}{2}$αβ,
n=α+β-m-2=α+β-$\frac{1}{2}$αβ-2;
(2)∵(2-α)(2-β)=4-2(α+β)+αβ=-2n≤0(n≥0),
又α≤β,
∴α≤2≤β;
(3)若使m+n=$\frac{13}{4}$成立,只需α+β=m+n+2=$\frac{13}{4}+2$=$\frac{21}{4}$①,
①当点M(α,β)在BC边上运动时,
由B(1,2),C(2,2),
得1≤α≤2,β=2,
而α=$\frac{21}{4}$-β=$\frac{13}{4}$>2,
故在BC边上存在满足条件的点,其坐标为($\frac{13}{4}$,2)所以不符合题意舍去;
即在BC边上不存在满足条件的点;
②当点M(α,β)在AC边上运动时,
由A(2,4),C(2,2),
得α=2,2≤β≤4,
此时β=$\frac{21}{4}$-α=$\frac{13}{4}$,
又因为2<$\frac{13}{4}$<4,
故在AC边上存在满足条件的点,其坐标为(2,$\frac{13}{4}$);
③当点M(α,β)在AB边上运动时,
由A(2,4),B(1,2),
得1≤α≤2,2≤β≤4,
由平面几何知识得,$\frac{2-α}{2-1}=\frac{4-β}{4-2}$,
于是β=2α②,
联立①②,解得α=$\frac{7}{4}$,β=$\frac{7}{2}$,
又因为1<$\frac{7}{4}$<2,2<$\frac{7}{2}$<4,
故在AB边上存在满足条件的点,其坐标为($\frac{7}{4}$,$\frac{7}{2}$).
综上所述,当点M(α,β)在△ABC的三条边上运动时,存在点(2,$\frac{13}{4}$)和点($\frac{7}{4}$,$\frac{7}{2}$),使m+n=$\frac{13}{4}$成立.
点评 此题是三角形综合题,主要考查了将根与系数的关系、根的判别式与动点问题相结合,体现了运动变化的观点,分类类讨论是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 0.25是0.5的一个平方根 | |
| B. | 正数有两个平方根,且这两个平方根之和等于0 | |
| C. | 72的平方根是7 | |
| D. | 负数有一个平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.
如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
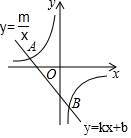 如图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
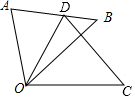 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )| A. | 40° | B. | 30° | C. | 38° | D. | 15° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com