
在△ABC中,AB=AC,∠BAC=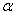 (
(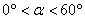 ),将线段BC绕点B逆时针旋转60°得到线段BD.
),将线段BC绕点B逆时针旋转60°得到线段BD.

(1)如图1,直接写出∠ABD的大小(用含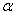 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求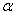 的值.
的值.
(1)∠ABD=30°-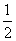 α;(2)△ABE是等边三角形;证明见解析;(3)30°.
α;(2)△ABE是等边三角形;证明见解析;(3)30°.
【解析】(1)∵AB=AC,∠A=α,∴∠ABC=∠ACB=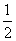 (180°-∠A)=90°-
(180°-∠A)=90°-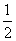 α,
α,
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,即∠ABD=30°-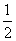 α;
α;
(2)△ABE是等边三角形,
连接AD,CD,ED,
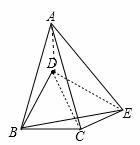
∵线段BC绕B逆时针旋转60°得到线段BD,则BC=BD,∠DBC=60°,∵∠ABE=60°,
∴∠ABD=60°-∠DBE=∠EBC=30°-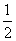 α,且△BCD为等边三角形,
α,且△BCD为等边三角形,
在△ABD与△ACD中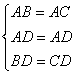 ,∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD=
,∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD=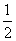 ∠BAC=
∠BAC=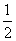 α,∵∠BCE=150°,∴∠BEC=180°-(30°-
α,∵∠BCE=150°,∴∠BEC=180°-(30°-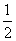 α)-150°=
α)-150°=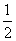 α=∠BAD,在△ABD和△EBC中
α=∠BAD,在△ABD和△EBC中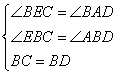 ,∴△ABD≌△EBC(AAS),∴AB=BE,∴△ABE是等边三角形;
,∴△ABD≌△EBC(AAS),∴AB=BE,∴△ABE是等边三角形;
(3)∵∠BCD=60°,∠BCE=150°,∴∠DCE=150°-60°=90°,∵∠DEC=45°,
∴△DEC为等腰直角三角形,∴DC=CE=BC,∵∠BCE=150°,∴∠EBC=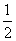 (180°-150°)=15°,∵∠EBC=30°-
(180°-150°)=15°,∵∠EBC=30°-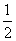 α=15°,∴α=30°.
α=15°,∴α=30°.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
预习练2-1:若一个三角形的三个内角的度数分别是40°,60°,80°,那么这个三角形是()
A、直角三角形
B、锐角三角形
C、钝角三角形
D、等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
11、如图,在△ABC沿直线BA翻折至△ABD和△ABD 全等三角形(填“是”“不是”);若CB=5,则DB= ;若△ABC的面积为10,则△ABD 的面积是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
一艘船从某港口A出发,以10nmile/h的速度向正北航行,从港口A出测得一礁石C在北偏西30度的方向上,如果这 艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上。(1)画出礁石C的位置;(2)求出小岛B与礁石C的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N,P、Q分别是弧AM、弧BM上一点(不与端点重合).若∠MNP=∠MNQ,下面结论:
①∠PNA=∠QNB;②∠P+∠Q=180°;③∠Q=∠PMN;④PM=QM;⑤MN2=PN•QN.
正确的结论有( )
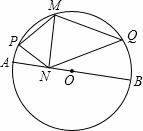
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,  为线段
为线段 上一动点(不与点
上一动点(不与点 重合),在
重合),在 同侧分别作正
同侧分别作正 和正
和正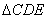 ,
, 与
与 交于点
交于点 ,
, 与
与 交于点
交于点 ,
, 与
与 交于点
交于点 ,连结
,连结 .以下五个结论:
.以下五个结论:
① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ;⑥
;⑥ .一定成立的结论有 (把你认为正确的序号都填上)
.一定成立的结论有 (把你认为正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.
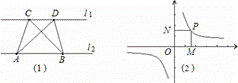

第二学习小组发现:如图(2),点P是反比例函数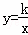 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
请利用上述结论解决下列问题:
(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则 =
=
_________.
(2)如图(4),点P、Q在反比例函数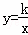 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若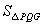 =8,则
=8,则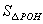 =_________,k=_________.
=_________,k=_________.
(3)如图(5)点P、Q是第一象限的点,且在反比例函数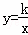 图象上,过点P作x轴垂线,过点Q作y轴
图象上,过点P作x轴垂线,过点Q作y轴
垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com