
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.
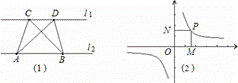

第二学习小组发现:如图(2),点P是反比例函数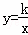 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
请利用上述结论解决下列问题:
(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则 =
=
_________.
(2)如图(4),点P、Q在反比例函数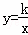 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若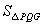 =8,则
=8,则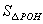 =_________,k=_________.
=_________,k=_________.
(3)如图(5)点P、Q是第一象限的点,且在反比例函数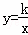 图象上,过点P作x轴垂线,过点Q作y轴
图象上,过点P作x轴垂线,过点Q作y轴
垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
科目:初中数学 来源: 题型:
 某市的水果加工厂P恰好在两条铁路OA、OB的夹角内部,为了抓住这个千载难逢的机遇,提高水果的销量,经理决定在这两条铁路沿线上各建一个运转站M、N,把加工厂的水果每天从加工厂P运往M、N请问M、N应建在何处,能够使P、M、N之间运转的路程最短.
某市的水果加工厂P恰好在两条铁路OA、OB的夹角内部,为了抓住这个千载难逢的机遇,提高水果的销量,经理决定在这两条铁路沿线上各建一个运转站M、N,把加工厂的水果每天从加工厂P运往M、N请问M、N应建在何处,能够使P、M、N之间运转的路程最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第ts时,△EFG的面积为Scm2.


(1)当 =1s时,S的值是多少?
=1s时,S的值是多少?
(2) 当 时,点E、F、G分别在边AB、BC、CD上移动,用含t的代数式表示S;当
时,点E、F、G分别在边AB、BC、CD上移动,用含t的代数式表示S;当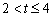 时,点E在边AB上移动,点F、G都在边CD上移动,用含t的代数式表示S.
时,点E在边AB上移动,点F、G都在边CD上移动,用含t的代数式表示S.
(3)若点F在矩形的边BC上移动,当 为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶
为何值时,以点B、E、F为顶点的三角形与以C、F、G为顶 点的三角形相似?请说明理由
点的三角形相似?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,AB=AC,∠BAC=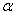 (
(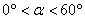 ),将线段BC绕点B逆时针旋转60°得到线段BD.
),将线段BC绕点B逆时针旋转60°得到线段BD.

(1)如图1,直接写出∠ABD的大小(用含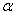 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求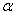 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com