16、如图，已知△ABC≌△ADE，∠DAC=60°，∠BAE=100° ，BC，DE相较于点F，求∠DFB的度数。
解析：∵△ABC≌△ADE
∴∠B=∠D，∠C=∠E,∠BAC=∠DAE
又∵∠DAC=60°，∠BAE=100°
∴∠DAB=∠BAE-∠BAC,∠CAE=∠BAE-∠DAE
∴∠DAB=∠CAE=（100°-60°）/2=20°
在△AGB和△FGD中,
∵∠B=∠D,∠BGF=∠DGF(对顶角相等)，
∴∠DFB=∠BAD=20°
科目：初中数学 来源： 题型：
11、如图，在△ABC沿直线BA翻折至△ABD和△ABD 全等三角形（填“是”“不是”）；若CB=5,则DB= ；若△ABC的面积为10，则△ABD 的面积是 。
查看答案和解析>>
科目：初中数学 来源： 题型：
2、已知等式
(1)(-a)^3.(-a)^2.(-a)=a^6
(2)(-a)^2.(-a).(-a)^4=a^7
(3)(-a)^2.(-a)^3.(-a)^2=a^7
(4)(-a^2).(-a^3).(-a)^3=-a^8
其中正确的是（）
A、（1）（2） B、（2）（3） C、（1）（4） D、（3）（4）
查看答案和解析>>
科目：初中数学 来源： 题型：
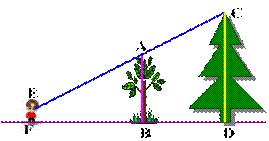
如图，小明为测量树CD的高度，先测量了两棵树根部之间的
距离BD=5m，已知树高AB=8m,站在点F处正好能望见CD的顶部，测得FB=8米，小明眼睛离地面的高度EF为1．6m，问树CD多高？
查看答案和解析>>
科目：初中数学 来源： 题型：
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究．
第一学习小组发现：如图（1），点A、点B在直线l1上，点C、点D在直线l2上，若l1∥l2，则S△ABC=S△ABD；反之亦成立．
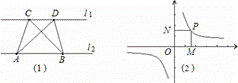
第二学习小组发现：如图（2），点P是反比例函数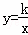
上任意一点，过点P作x轴、y轴的垂线，垂足为M、N，则矩形OMPN的面积为定值|k|．
请利用上述结论解决下列问题：
（1）如图（3），四边形ABCD、与四边形CEFG都是正方形点E在CD上，正方形ABCD边长为2，则
=
_________．
（2）如图（4），点P、Q在反比例函数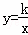图象上，PQ过点O，过P作y轴的平行线交x轴于点H，过Q作x轴的平行线交PH于点G，若
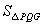=8，则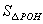
=_________，k=_________．
（3）如图（5）点P、Q是第一象限的点，且在反比例函数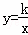图象上，过点P作x轴垂线，过点Q作y轴
垂线，垂足分别是M、N，试判断直线PQ与直线MN的位置关系，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
