
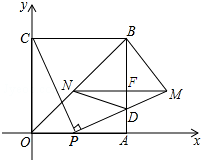
 如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.分析 (1)作ME⊥x轴于E,根据正方形的性质和题意证明△MPE≌△PCO,得到ME=PO=t,EP=OC=2,得到答案;
(2)连接AM,证明矩形AEMF是正方形和四边形OAMN是平行四边形,得到MN=OA,得到答案;
(3)根据相似三角形的性质求出BD的长,根据四边形BMDN的面积S=$\frac{1}{2}$MN•BD计算即可.
解答 解:(1)作ME⊥x轴于E,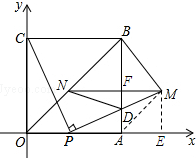 则∠MEP=90°,ME∥AB,
则∠MEP=90°,ME∥AB,
∴∠MPE+∠PME=90°,
∵四边形OABC是正方形,
∴∠POC=90°,OA=OC=AB=BC=4,∠BOA=45°,
∵PM⊥CP,
∴∠MPE+∠CPO=90°,
∴∠PME=∠CPO,
在△MPE和△PCO中,
$\left\{\begin{array}{l}{∠MEP=∠POC}\\{∠PME=∠CPO}\\{PM=CP}\end{array}\right.$,
∴△MPE≌△PCO(AAS),
∴ME=PO=t,EP=OC=2,
∴OE=t+2,
∴M(t+2,t);
(2)线段MN的长度不发生改变;
理由如下:连接AM,
∵MN∥OA,ME∥AB,∠MEA=90°,
∴四边形AEMF是矩形.
又∵EP=OC=OA,
∴AE=PO=t=ME,
∴矩形AEMF是正方形.
∴∠MAE=45°=∠BOA,
∴AM∥OB,
又∵MN∥OA,
∴四边形OAMN是平行四边形,
∴MN=OA=2(为定值);
(3)∵OP=$\sqrt{2}$AP,OA=2,
∴$\sqrt{2}$AP+AP=2,
解得AP=2($\sqrt{2}$-1),
∴t=OP=2-2($\sqrt{2}$-1)=2(2-$\sqrt{2}$),
∵ME∥AB,
∴△PAD∽△PEM,
∴$\frac{AD}{EM}$=$\frac{PA}{PE}$,即$\frac{AD}{t}$=$\frac{2-t}{2}$,
∴AD=-$\frac{1}{2}$t2+t=-$\frac{1}{2}$×[2(2-$\sqrt{2}$)]2+2(2-$\sqrt{2}$)=6$\sqrt{2}$-8,
∴BD=AB-AD=2-(6$\sqrt{2}$-8)=10-6$\sqrt{2}$,
∵MN∥OA,AB⊥OA,
∴MN⊥AB,
∴四边形BMDN的面积S=$\frac{1}{2}$MN•BD,
=$\frac{1}{2}$×2×(10-6$\sqrt{2}$)
=10-6$\sqrt{2}$.
点评 本题考查的是正方形的性质、相似三角形的判定和性质、全等三角形的判定和性质,掌握相关的判定定理和性质定理、正确作出辅助线是解题的关键,注意坐标与图形的关系的应用以及四边形的面积公式的应用.


科目:初中数学 来源: 题型:解答题
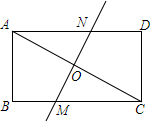 如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.
如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
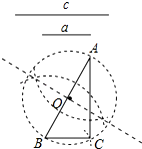 数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:
数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:| A. | 勾股定理 | B. | 直径所对的圆周角是直角 | ||
| C. | 勾股定理的逆定理 | D. | 90°的圆周角所对的弦是直径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
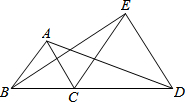 已知,△ABC和△CDE都是等边三角形,
已知,△ABC和△CDE都是等边三角形,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{{\sqrt{3}}}{2}$,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,-$\frac{{\sqrt{3}}}{2}$) | C. | ($\frac{{\sqrt{3}}}{2}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com