
| A. | (-$\frac{{\sqrt{3}}}{2}$,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,-$\frac{{\sqrt{3}}}{2}$) | C. | ($\frac{{\sqrt{3}}}{2}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$) |
分析 根据中点定义求出OP的长度,再根据旋转的性质求出OQ的长度,过点Q作QC⊥OB于点C,然后通过解直角三角形求出OC、QC的长度,即可得到点Q的坐标.
解答 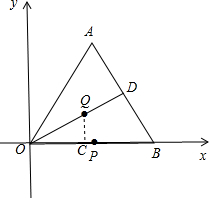 解:∵O(0,0)、A(1,$\sqrt{3}$)、B(2,0),
解:∵O(0,0)、A(1,$\sqrt{3}$)、B(2,0),
点P是线段OB的中点,
∴P(1,0),
根据旋转变换的性质,OQ=OP=1,
过点Q作QC⊥OB于点C,
则OC=OQ•cos30°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
QC=OQ•sin30°=1×$\frac{1}{2}$=$\frac{1}{2}$,
∴点Q的坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).
故选C.
点评 本题考查了坐标与图形的变化-旋转以及解直角三角形,作出图形更形象直观.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
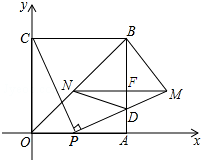 如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
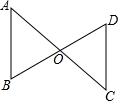 如图,已知OA=OC,OB=OD.
如图,已知OA=OC,OB=OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
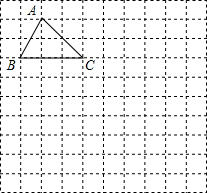 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法).
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
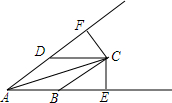 如图,点D、B分别在∠A的两边上,过点B作BC∥AD,过点D作DC∥AB交BC于点C,过点C分别作∠A两边的垂线,垂足分别为E、F,若BC=DC,求证:点C在∠A的平分线上.
如图,点D、B分别在∠A的两边上,过点B作BC∥AD,过点D作DC∥AB交BC于点C,过点C分别作∠A两边的垂线,垂足分别为E、F,若BC=DC,求证:点C在∠A的平分线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -x(x2-x+1)=x3-x2-x | B. | (-2x)3•x2=-8x6 | ||
| C. | m(m+n)-n(m+n)=m2-n2 | D. | -xm(xn-x3+3)=-xmn+x3m-3xm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com