
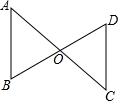
 如图,已知OA=OC,OB=OD.
如图,已知OA=OC,OB=OD.分析 已知条件OA=OC,OB=OD,再加上对顶角∠COD=∠AOB可利用SAS证明△DOC≌△BOA进而得到∠A=∠C,根据平行线的判定可得DC∥AB.
解答 证明:在△AOB和△COD中,
$\left\{\begin{array}{l}{OA=OC}\\{∠AOB=∠COD}\\{OB=OD}\end{array}\right.$,
∴△DOC≌△BOA(SAS),
∴∠A=∠C,
∴DC∥AB(内错角相等,两直线平行),
故答案为:SAS;∠C;内错角相等,两直线平行.
点评 此题主要考查了全等三角形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
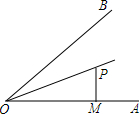 如图,若∠AOB的平分线上一点P到OA的距离PM等于5,N是射线OB上的任一点,则关于PN的长( )
如图,若∠AOB的平分线上一点P到OA的距离PM等于5,N是射线OB上的任一点,则关于PN的长( )| A. | PN>5cm | B. | PN<5cm | C. | PN≥5cm | D. | PN≤5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
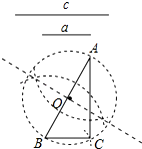 数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:
数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:| A. | 勾股定理 | B. | 直径所对的圆周角是直角 | ||
| C. | 勾股定理的逆定理 | D. | 90°的圆周角所对的弦是直径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
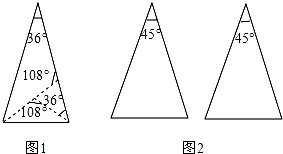 阅读下列材料,完成相关问题:
阅读下列材料,完成相关问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{{\sqrt{3}}}{2}$,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,-$\frac{{\sqrt{3}}}{2}$) | C. | ($\frac{{\sqrt{3}}}{2}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com