
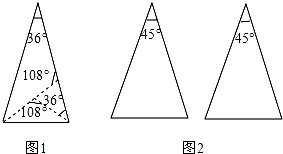
 �Ķ����в��ϣ����������⣺
�Ķ����в��ϣ����������⣺���� ��1��45����Ȼ�뵽����ֱ�������Σ�����һ�������Աߵĸߣ������γ�һ������ֱ�������κ�ֱ�������Σ�ֱ��������б�ߵ����߿��γ��������������Σ�����һ��������ڶ������ο��Կ��������и����ķ���������ͬ����һ����Ϊ�µ��������εĵǣ�����һ�ű���Ϊ45���22.5�㣬����22.5��ֱ���Ϊ���������εĵǻǣ���������Ϊ��ʱ���õ�����������ǡ��Ϊ���������Σ�����һ������������
��2������������ֱ�߱���30��ǣ�����ȷ��һ��ΪBA��һ��ΪBC��������������ȹ̶�BA�ij��������ȷ��D�㣬�ٱ���ͼʵ��--�ֱ���ADΪ���������ε������ߵױߣ����A��E��C��ͬһֱ���ϣ���2��������ABC������ͼ����x��ֵ��
��� �⣺��1����ͼ2��ͼ��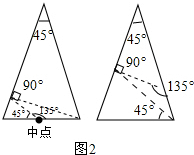
��2����ͼ3 �١�������ABC��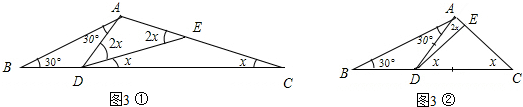
�ٵ�AD=AEʱ��
��2x+x=30+30��
��x=20��
�ڵ�AD=DEʱ��
��30+30+2x+x=180��
��x=40��
���ԡ�C�Ķ�����20���40�㣮
���� ���⿼����ѧ��ѧϰ���������������ִ���������֪ʶ�����ص㿼���������ڽǡ���Ǽ�Ĺ�ϵ������������֪ʶ����һ���ܶ���ѧ����������Ŀ��


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�AC=2����BAC=75�㣬��C=60�㣬��BE��AE�ཻ��H����DH�ij�Ϊ��������
��ͼ���ڡ�ABC�У�AC=2����BAC=75�㣬��C=60�㣬��BE��AE�ཻ��H����DH�ij�Ϊ��������| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
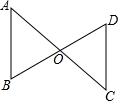 ��ͼ����֪OA=OC��OB=OD��
��ͼ����֪OA=OC��OB=OD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
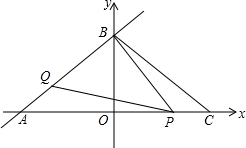 ��ͼ��ֱ��l��y=$\frac{3}{4}x+$3��x��y��ֱ�ΪA��B���㣬C����A�����y��Գƣ�����P��Q�ֱ����߶�AC��AB�ϣ���P�����A��C�غϣ��������BPQ=��BAO��
��ͼ��ֱ��l��y=$\frac{3}{4}x+$3��x��y��ֱ�ΪA��B���㣬C����A�����y��Գƣ�����P��Q�ֱ����߶�AC��AB�ϣ���P�����A��C�غϣ��������BPQ=��BAO���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com