
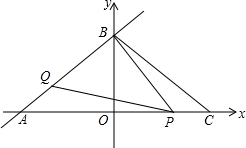
 如图,直线l:y=$\frac{3}{4}x+$3交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
如图,直线l:y=$\frac{3}{4}x+$3交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.分析 (1)对于直线l解析式,分别令x与y为0求出y与x的值,确定出A与B的坐标,根据A与C关于y轴对称确定出C坐标,利用勾股定理求出BC的长即可;
(2)由三角形APQ与三角形CBP全等,利用全等三角形对应边相等得到PQ=BC=5,由AP-OA=OP,求出OP的长,确定出P坐标即可;
(3)分三种情况考虑:当PQ=PB时,由(2)确定出此时P的坐标;当BQ=BP时,利用外角性质判断不可能;当BQ=PQ时,求出此时P的坐标即可.
解答 解:(1)对于直线l:y=$\frac{3}{4}$x+3,
令x=0,得到y=3;令y=0,得到x=-4,
∴A(-4,0),B(0,3),即OB=3,
∵A与C关于y轴对称,
∴C(4,0),即OC=4,
则根据勾股定理得:BC=$\sqrt{{3}^{2}+{4}^{2}}$=5;
故答案为:(-4,0);(0,3);5;
(2)由△APQ≌△CBP,得到AP=BC=5,
∵A(-4,0),即OA=4,
∴OP=5-4=1,即P(1,0);
(3)(i)当PQ=PB时,△APQ≌△CBP,
由(2)知此时点P(1,0);
(ii)当BQ=BP时,∠BQP=∠BPQ,
∵∠BQP是△APQ的外角,
∴∠BQP>∠BAP,
又∵∠BPQ=∠BAO,
∴这种情况不可能;
(iii)当BQ=PQ时,∠QBP=∠QPB,
又∵∠BPQ=∠BAO,
∴∠QBP=∠BAO,
∴AP=4+x,BP=$\sqrt{{x}^{2}+{3}^{2}}$,
∴4+x=$\sqrt{{x}^{2}+9}$,
解得:x=-$\frac{7}{8}$.
此时点P的坐标为:(-$\frac{7}{8}$,0).
综上,P的坐标为(1,0),(-$\frac{7}{8}$,0).
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,坐标与图形性质,等腰三角形的性质,全等三角形的判定与性质,熟练掌握性质与判定是解本题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
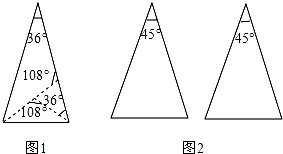 阅读下列材料,完成相关问题:
阅读下列材料,完成相关问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
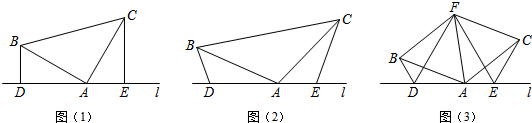
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
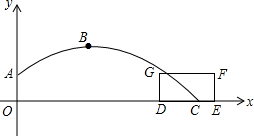 在体育测试时,初三的一名高个子男生推铅球,铅球的运动轨迹ABC可看作某条抛物线的一部分,已知这名男生的出手处A点离地面的高度为2米,当球运动到最高处5米时,离该男生站立地点O的水平距离为6米.以O为原点建立如图所示的坐标系.
在体育测试时,初三的一名高个子男生推铅球,铅球的运动轨迹ABC可看作某条抛物线的一部分,已知这名男生的出手处A点离地面的高度为2米,当球运动到最高处5米时,离该男生站立地点O的水平距离为6米.以O为原点建立如图所示的坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com