
分析 令a为0和1之间的一个数,然后按照题目要求进行运算,从而可发现其中的规律.
解答 解:令a=$\frac{1}{2}$,则b=$(\frac{1}{2})^{2}-1$=$\frac{1}{4}-1$=-$\frac{3}{4}$;
c=$(-\frac{3}{4})^{2}$-1=$\frac{9}{16}$-1=-$\frac{7}{16}$;
d=$(-\frac{7}{16})^{2}-1$=$\frac{49}{256}-1$=-$\frac{205}{356}$;
随着运算次数的增加,结果越接近-1.
点评 本题主要考查的是数字的变化规律,取特殊值法的应用是解题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
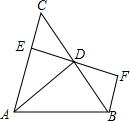 如图,AD是△ABC的高,BF∥AC,过D点的直线交AC于点E,交BF于点F,DE=DF.
如图,AD是△ABC的高,BF∥AC,过D点的直线交AC于点E,交BF于点F,DE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
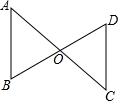 如图,已知OA=OC,OB=OD.
如图,已知OA=OC,OB=OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
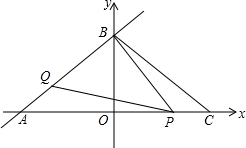 如图,直线l:y=$\frac{3}{4}x+$3交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
如图,直线l:y=$\frac{3}{4}x+$3交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
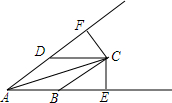 如图,点D、B分别在∠A的两边上,过点B作BC∥AD,过点D作DC∥AB交BC于点C,过点C分别作∠A两边的垂线,垂足分别为E、F,若BC=DC,求证:点C在∠A的平分线上.
如图,点D、B分别在∠A的两边上,过点B作BC∥AD,过点D作DC∥AB交BC于点C,过点C分别作∠A两边的垂线,垂足分别为E、F,若BC=DC,求证:点C在∠A的平分线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com