
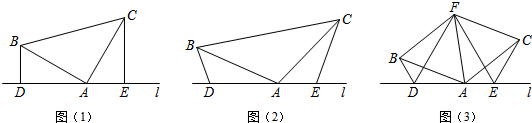
���� ��1����������֤����ABD�ա�CAE���ɵ�DA=CE��AE=BD���ɵ�DE=BD+CE��
��2����������֪��BAD+��CAE=180��-�����ҡ�DBA+��BAD=180��-�����ɵá�DBA=��CAE�����������֤����ABD�ա�CAE��ͬ��1���ɵó����ۣ�
��3���ɣ�2��֪����ADB�ա�CAE���õ�BD=EA����DBA=��CAE���١�DBF�ա�EAF��SAS�����õ�DF=EF����BFD=��AFE�������DFE=��DFA+��AFE=��DFA+��BFD=60�㣬���ԡ�DEFΪ�ȱ������Σ����ɵõ�DF=EF��
��� �⣺��1����BD��l��CE��l��
���BDA=��AEC=90��
�֡ߡ�BAC=90�㣬
���BAD+��CAE=90�㣬��BAD+��ABD=90�㣬
���CAE=��ABD
�ڡ�ABD�͡�CAE�У�
$\left\{\begin{array}{l}{��ABD=��CAE}\\{��ADB=��CEA=9{0}^{��}}\\{AB=AC}\end{array}\right.$��
���ABD�ա�CAE��AAS��
��BD=AE��AD=CE��
��DE=AD+AE��
��DE=CE+BD��
��2������
�ߡ�BDA=��AEC=��BAC=����
���DBA+��BAD=��BAD+��CAE=180��-����
���CAE=��ABD��
�ڡ�ADB�͡�CEA�У�
$\left\{\begin{array}{l}{��ABD=��CAE}\\{��ADB=��CEA}\\{AB=AC}\end{array}\right.$��
���ADB�ա�CEA��AAS����
��AE=BD��AD=CE��
��BD+CE=AE+AD=DE��
��3���ɣ�2��֪����ADB�ա�CAE��
��BD=EA����DBA=��CAE��
�ߡ�ABF�͡�ACF��Ϊ�ȱ������Σ�
���ABF=��CAF=60�㣬
���DBA+��ABF=��CAE+��CAF��
���DBF=��FAE��
��BF=AF
�ڡ�DBF�͡�EAF�У�
$\left\{\begin{array}{l}{FB=FA}\\{��FBD=��FAE}\\{BD=AE}\end{array}\right.$��
���DBF�ա�EAF��SAS����
��DF=EF����BFD=��AFE��
���DFE=��DFA+��AFE=��DFA+��BFD=60�㣬
���DEFΪ�ȱ������Σ�
��DF=EF��
���� ������Ҫ����ȫ�������ε��ж������ʣ�������֤��������ȫ���ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
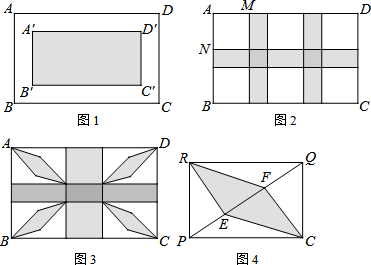
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
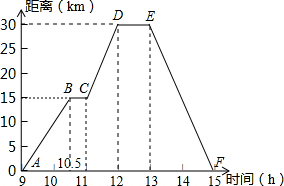 Сǿ�����г�ȥ���Σ���ͼ��ʾ����ҵľ���y��ǧ�ף������õ�ʱ��x��Сʱ��֮���ϵ�ĺ���ͼ��С��9���뿪�ң�15��ؼң��������ͼ������ش��������⣺
Сǿ�����г�ȥ���Σ���ͼ��ʾ����ҵľ���y��ǧ�ף������õ�ʱ��x��Сʱ��֮���ϵ�ĺ���ͼ��С��9���뿪�ң�15��ؼң��������ͼ������ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
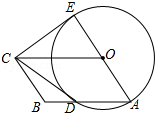 ��ͼ���ı���OABC��ƽ���ı��Σ���OΪԲ�ģ�OAΪ�뾶��Բ��AB��D���ӳ�AO����O��E������CD��CE����CE�ǡ�O�����ߣ�
��ͼ���ı���OABC��ƽ���ı��Σ���OΪԲ�ģ�OAΪ�뾶��Բ��AB��D���ӳ�AO����O��E������CD��CE����CE�ǡ�O�����ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
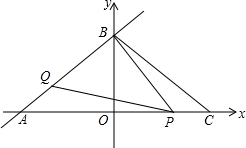 ��ͼ��ֱ��l��y=$\frac{3}{4}x+$3��x��y��ֱ�ΪA��B���㣬C����A�����y��Գƣ�����P��Q�ֱ����߶�AC��AB�ϣ���P�����A��C�غϣ��������BPQ=��BAO��
��ͼ��ֱ��l��y=$\frac{3}{4}x+$3��x��y��ֱ�ΪA��B���㣬C����A�����y��Գƣ�����P��Q�ֱ����߶�AC��AB�ϣ���P�����A��C�غϣ��������BPQ=��BAO���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
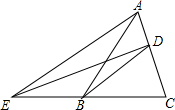 ��ͼ����ABC�����Ϊ6��DΪAC����һ�㣬AD=$\frac{1}{2}$CD������BD������A��DB��ƽ���߽�CB���ӳ����ڵ�E������DE�����EDB�������
��ͼ����ABC�����Ϊ6��DΪAC����һ�㣬AD=$\frac{1}{2}$CD������BD������A��DB��ƽ���߽�CB���ӳ����ڵ�E������DE�����EDB��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com