
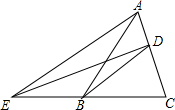
 如图.△ABC的面积为6,D为AC边上一点,AD=$\frac{1}{2}$CD,连接BD.过点A作DB的平行线交CB的延长线于点E,连接DE,求△EDB的面积.
如图.△ABC的面积为6,D为AC边上一点,AD=$\frac{1}{2}$CD,连接BD.过点A作DB的平行线交CB的延长线于点E,连接DE,求△EDB的面积. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
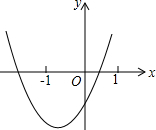 二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )| A. | ab<0 | B. | bc>0 | C. | a+b+c>0 | D. | a-b+c>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
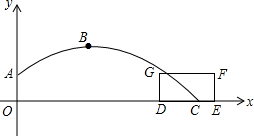 在体育测试时,初三的一名高个子男生推铅球,铅球的运动轨迹ABC可看作某条抛物线的一部分,已知这名男生的出手处A点离地面的高度为2米,当球运动到最高处5米时,离该男生站立地点O的水平距离为6米.以O为原点建立如图所示的坐标系.
在体育测试时,初三的一名高个子男生推铅球,铅球的运动轨迹ABC可看作某条抛物线的一部分,已知这名男生的出手处A点离地面的高度为2米,当球运动到最高处5米时,离该男生站立地点O的水平距离为6米.以O为原点建立如图所示的坐标系.查看答案和解析>>
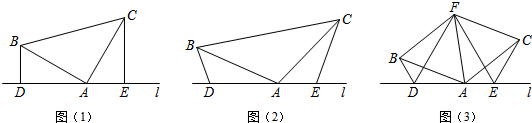
科目:初中数学 来源: 题型:选择题
| A. | S1>S2>S3 | B. | S2>S1>S3 | C. | S3>S1>S2 | D. | S3>S2>S1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com