
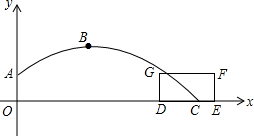
 ����������ʱ��������һ���߸���������Ǧ��Ǧ����˶��켣ABC�ɿ���ij�������ߵ�һ���֣���֪���������ij��ִ�A�������ĸ߶�Ϊ2�ף������˶�����ߴ�5��ʱ���������վ���ص�O��ˮƽ����Ϊ6�ף���OΪԭ�㽨����ͼ��ʾ������ϵ��
����������ʱ��������һ���߸���������Ǧ��Ǧ����˶��켣ABC�ɿ���ij�������ߵ�һ���֣���֪���������ij��ִ�A�������ĸ߶�Ϊ2�ף������˶�����ߴ�5��ʱ���������վ���ص�O��ˮƽ����Ϊ6�ף���OΪԭ�㽨����ͼ��ʾ������ϵ������ ��1�����������֪��A��0��2����B��6��5�����������ߵĶԳ��Կ�֪�����߾����㣨12��2����Ȼ�����ô���ϵ������⼴�ɣ�
��2����y=0�����������x�ύ������꣬�Ӷ�����õ�O����C�ľ��룻
��3����y=$\frac{11}{12}$�������x��ֵ��Ȼ����ݿ�ij�DE=1���Ӷ���ȷ����m��ȡֵ��Χ��
��� �⣺��1�����������֪��A��0��2����B��6��5�����������ߵĶԳ��Կ�֪�����߾����㣨12��2����
�������ߵĽ���ʽΪy=ax2+bx+c������0��2������6��5������12��2������ã�$\left\{\begin{array}{l}{c=2}\\{36a+6b+c=5}\\{144a+12b+c=2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-\frac{1}{12}}\\{b=1}\\{c=2}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{1}{12}$x2+x+2��
��2����y=0�ã�-$\frac{1}{12}$x2+x+2=0��
��ã�x1=6+2$\sqrt{15}$��x2=6-2$\sqrt{15}$����ȥ����
�𣺸�������Ǧ���Ƴ�ȥ6+2$\sqrt{15}$��Զ��
��3����y=$\frac{11}{12}$�ã�-$\frac{1}{12}$x2+x+2=$\frac{11}{12}$��
��ã�x1=13��x2=-1����ȥ����
��DE=1��
��12��m��13��
���� ������Ҫ������Ƕ��κ�����Ӧ�ã��ҳ������߾����ĵ�����꣬�Ӷ��õ������ߵĽ���ʽ�ǽ���Ĺؼ���


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
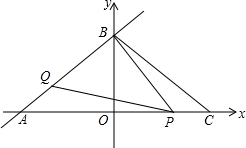 ��ͼ��ֱ��l��y=$\frac{3}{4}x+$3��x��y��ֱ�ΪA��B���㣬C����A�����y��Գƣ�����P��Q�ֱ����߶�AC��AB�ϣ���P�����A��C�غϣ��������BPQ=��BAO��
��ͼ��ֱ��l��y=$\frac{3}{4}x+$3��x��y��ֱ�ΪA��B���㣬C����A�����y��Գƣ�����P��Q�ֱ����߶�AC��AB�ϣ���P�����A��C�غϣ��������BPQ=��BAO���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
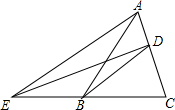 ��ͼ����ABC�����Ϊ6��DΪAC����һ�㣬AD=$\frac{1}{2}$CD������BD������A��DB��ƽ���߽�CB���ӳ����ڵ�E������DE�����EDB�������
��ͼ����ABC�����Ϊ6��DΪAC����һ�㣬AD=$\frac{1}{2}$CD������BD������A��DB��ƽ���߽�CB���ӳ����ڵ�E������DE�����EDB��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$�� | B�� | 1�� | C�� | 2�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com