
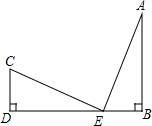
 如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:CE⊥AE.
如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:CE⊥AE. 分析 根据SAS证△EDC≌△ABE,推出∠CED=∠A,根据∠B=90°求出∠A+∠AEB=90°,推出∠CED+∠AEB=90°,求出∠CEA=90°即可.
解答 解:∵CD⊥DE,AB⊥DB,
∴∠D=∠B=90°,
在△EDC和△ABE中
∵$\left\{\begin{array}{l}{CD=BE}\\{∠D=∠B}\\{DE=AB}\end{array}\right.$,
∴△EDC≌△ABE(SAS),
∴∠CED=∠A,
∵∠B=90°,
∴∠A+∠AEB=90°,
∴∠CED+∠AEB=90°,
∴∠CEA=90°,
∴CE⊥AE.
点评 本题考查了全等三角形的性质和判定,三角形的内角和定理,全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应角相等,解决本题的关键是证明三角形全等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
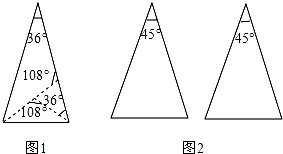 阅读下列材料,完成相关问题:
阅读下列材料,完成相关问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
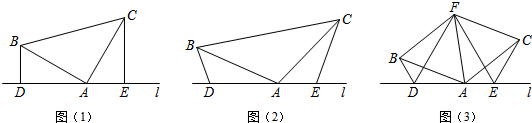
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
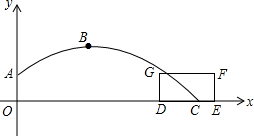 在体育测试时,初三的一名高个子男生推铅球,铅球的运动轨迹ABC可看作某条抛物线的一部分,已知这名男生的出手处A点离地面的高度为2米,当球运动到最高处5米时,离该男生站立地点O的水平距离为6米.以O为原点建立如图所示的坐标系.
在体育测试时,初三的一名高个子男生推铅球,铅球的运动轨迹ABC可看作某条抛物线的一部分,已知这名男生的出手处A点离地面的高度为2米,当球运动到最高处5米时,离该男生站立地点O的水平距离为6米.以O为原点建立如图所示的坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com