
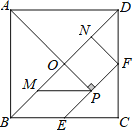
【题目】七巧板是一种古老的中国传统智力玩具.如图,在正方形纸板ABCD中,BD为对角线,E、F分别为BC、CD的中点,AP⊥EF分别交BD、EF于O、P两点,M、N分别为BO、DO的中点,连接MP、NF,沿图中实线剪开即可得到一副七巧板.若AB=1,则四边形BMPE的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据三角形的中位线的性质得到EF∥BD,EF=![]() BD,推出点P在AC上,得到PE=
BD,推出点P在AC上,得到PE=![]() EF,得到四边形BMPE平行四边形,过M作MF⊥BC于F,根据平行四边形的面积公式即可得到结论.
EF,得到四边形BMPE平行四边形,过M作MF⊥BC于F,根据平行四边形的面积公式即可得到结论.
∵E,F分别为BC,CD的中点,
∴EF∥BD,EF=![]() BD,
BD,
∵四边形ABCD是正方形,且AB=BC=1,
∴BD=![]() ,
,
∵AP⊥EF,
∴AP⊥BD,
∴BO=OD,
∴点P在AC上,
∴PE=![]() EF,
EF,
∴PE=BM,
∴四边形BMPE是平行四边形,
∴BO=![]() BD,
BD,
∵M为BO的中点,
∴BM=![]() BD=
BD=![]() ,
,
∵E为BC的中点,
∴BE=![]() BC=
BC=![]() ,
,
过M作MF⊥BC于F,
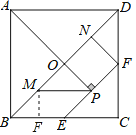
∴MF=![]() BM=
BM=![]() ,
,
∴四边形BMPE的面积=BEMF=![]() ,
,
故选B.


科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象过点A(﹣3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是﹣2.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为( )
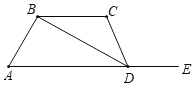
A.∠C+∠ADC=180°B.∠A+∠ABD=180°
C.∠CBD=∠ADCD.∠C=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一刻度尺放在数轴上.

①若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 5,则 1cm 对应数轴上的点表示的数是 2;
②若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为 1 和 9,则 1cm 对应数轴上的点表示的数是 3;
③若刻度尺上 0cm 和 4cm 对应数轴上的点表示的数分别为-2 和 2,则 1cm 对应数轴上的点表示的数是-1;
④若刻度尺上 0cm 和 4 cm 对应数轴上的点表示的数分别为-1 和 1,则 1cm 对应数轴上的点表示的数是-0.5. 上述结论中,所有正确结论的序号是 ( )
A.①②B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E是CD边上一点,![]() ,连接AE、BE、BD,且AE、BD交于点F.若
,连接AE、BE、BD,且AE、BD交于点F.若![]() ,则
,则![]() ( )
( )

A.15.5B.16.5C.17.5D.18.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD的面积为100,P为边CD上的任一点,E,F分别为线段AP,BP的中点,则图中阴影部分的总面积为( )

A. 30B. 25C. 22.5D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
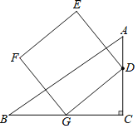
【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,点G为边BC的中点,点D从点C出发沿CA向点A运动,到点A停止,以GD为边作正方形DEFG,则点E运动的路程为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分类是研究问题的一种常用方法,我们在学习有理数和代数式的相关概念、运算法则时,除了 学到了具体知识,还学会了分类思考,在进行分类时,我们首先应明确分类标准,其次要做到分类时既不 重复,也不遗漏。
(初步感受)(1)在对多项式![]() ,
,![]() 进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
(简单运用)(2)已知 a, b 是有理数,比较 a b 与 a b的大小;
(深入思考)(3)已知 a, b c 是有理数,且 ca b>ca b ,判断 b, c 的符号,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com