
【题目】分类是研究问题的一种常用方法,我们在学习有理数和代数式的相关概念、运算法则时,除了 学到了具体知识,还学会了分类思考,在进行分类时,我们首先应明确分类标准,其次要做到分类时既不 重复,也不遗漏。
(初步感受)(1)在对多项式![]() ,
,![]() 进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
(简单运用)(2)已知 a, b 是有理数,比较 a b 与 a b的大小;
(深入思考)(3)已知 a, b c 是有理数,且 ca b>ca b ,判断 b, c 的符号,并说明理由。
【答案】(1)按项数分,分为 2 类,按次数分,分为 2 类;
(2)① ![]() 时,
时, ![]()
② ![]() 时,
时, ![]()
③ ![]() 时,
时, ![]()
(3) b,c同正或同负
【解析】
(1)可按照项数分类为二项式和三项式,按照次数分类为一次多项式和二次多项式即可;
(2)运用作差法![]() ,故只需要考虑b的取值即可判断大小;
,故只需要考虑b的取值即可判断大小;
(3)分类讨论:①![]() ;②
;②![]() ;③
;③![]() 三种情况讨论,即可得到c的取值范围,即可判断b、c的符号;或者直接计算解不等式分析即可.
三种情况讨论,即可得到c的取值范围,即可判断b、c的符号;或者直接计算解不等式分析即可.
解:(1)按项数分,分为 2 类
二项式:![]()
三项式: ![]()
按次数分,分为 2 类
一次多项式:![]()
二次多项式: ![]()
(2)![]()
① ![]() 时,
时,![]() ,∴
,∴![]()
② ![]() 时,
时,![]() ,∴
,∴![]()
③ ![]() 时,
时, ![]() ,∴
,∴![]()
(3)法一:解:①![]() 时 ,
时 , ![]() ,此时
,此时 ![]() (舍)
(舍)
②![]() 时 ,
时 ,
![]()
∵![]()
∴![]()
③b<0时,
![]()
![]()
![]()
综上: b,c同正或同负
法二:解:![]() ,
,
整理得:
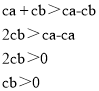
∴c、b同正或同负


科目:初中数学 来源: 题型:
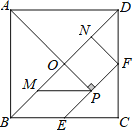
【题目】七巧板是一种古老的中国传统智力玩具.如图,在正方形纸板ABCD中,BD为对角线,E、F分别为BC、CD的中点,AP⊥EF分别交BD、EF于O、P两点,M、N分别为BO、DO的中点,连接MP、NF,沿图中实线剪开即可得到一副七巧板.若AB=1,则四边形BMPE的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3-1),B(-4,-3),C(-2,-3).
(1)画出将△ABC向上平移5个单位得到的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC关于点O成中心对称的图形△A2B2C2,并写出点B2的坐标;
(3)观察图形,△A1B1C1和△A2B2C2成中心对称吗?如果成中心对称,那么对称中心的坐标为_____;如果不成中心对称,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练,机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动,已知AD=6个单位长度,机器人的速度为1个单位长度/s且其移动至拐角处调整方向所需时间忽略不计.设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)图②中函数图象与纵轴的交点的纵坐标![]() 在图①中表示一条线段的长,请在图①中画出这条线段.
在图①中表示一条线段的长,请在图①中画出这条线段.
(2)求图②中a的值;
(3)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠3=∠E.试说明:∠A=∠EBC.(请按图填空,并补理由.)
证明:∵∠1=∠2 (已知),

∴________∥_______( ),
∴∠E=∠_______ ( ),
又∵∠E=∠3 (已知),
∴∠3=∠____________ ( 等量代换 ),
∴_________∥________ (内错角相等,两直线平行),
∴∠A=∠EBC ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面各图,寻找对顶角(不含平角)
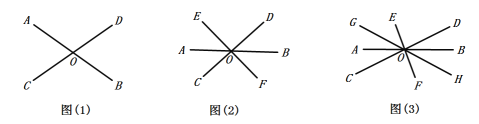
(1)如图(1),图中共有________对不同的对顶角.
(2)如图(2),图中共有________对不同的对顶角.
(3)如图(3),图中共有________对不同的对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有![]()
![]() 条直线相交于一点,则可形成________对不同的对顶角.
条直线相交于一点,则可形成________对不同的对顶角.
(5)计算2013条直线相交于一点,则可形成________对不同的对顶角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com