
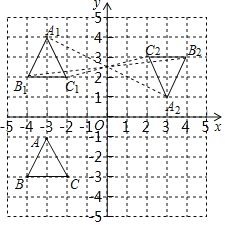
����Ŀ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-3-1����B��-4��-3����C��-2��-3����
��1����������ABC����ƽ��5����λ�õ�����A1B1C1����д����B1�����ꣻ
��2��������ABC���ڵ�O�����ĶԳƵ�ͼ����A2B2C2����д����B2�����ꣻ
��3���۲�ͼ�Σ���A1B1C1����A2B2C2�����ĶԳ�����������ĶԳƣ���ô�Գ����ĵ�����Ϊ_____������������ĶԳƣ���˵�����ɣ�

���𰸡���1����A1B1C1��Ϊ������������B1������Ϊ��-4��2������2����A2B2C2��Ϊ������������B2������Ϊ��4��3������3����0��2.5����
��������
��1�����������ƽ�Ƶ����ʻ�����������ABC����ƽ��5����λ�õ�����A1B1C1��Ȼ������ƽ�ƹ���д����B1�����ꣻ
��2��������������ĶԳƵ����ʻ�����ABC���ڵ�O�����ĶԳƵ�ͼ����A2B2C2��Ȼ���������ĶԳƹ���д����B2�����ꣻ
��3���������ĶԳƵ����ʼ�����⣮
�⣺��1����A1B1C1��Ϊ����B1������Ϊ��-4��2����
��2����A2B2C2������B2��������4��3����
��3����A1B1C1����A2B2C2�����ĶԳ��𣬶Գ����ĵ�����Ϊ��0��2.5����
�ʴ�Ϊ����0��2.5����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+bx+c��ͼ�����A����3��0���͵�B��1��0��������y�ύ�ڵ�C��D�������������Һ������ǩ�2��
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ�������һ����P�����PA+PD����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
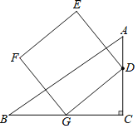
����Ŀ����ͼ����֪��ABCD�����Ϊ100,PΪ��CD�ϵ���һ�㣬E��F�ֱ�Ϊ�߶�AP��BP���е㣬��ͼ����Ӱ���ֵ������Ϊ�� ��

A. 30B. 25C. 22.5D. 20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C��90�㣬AB��5��BC��4����GΪ��BC���е㣬��D�ӵ�C������CA���A�˶�������Aֹͣ����GDΪ����������DEFG�����E�˶���·��Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˽�����������������ļ�ֵ������֪���̶ȣ���ȡ��������ķ�ʽ�����ʾ����飬��������Ϊ��A���dz��˽�������B���˽�������C�������˽��������ȼ��������ݵ���������������������������ͳ��ͼ��
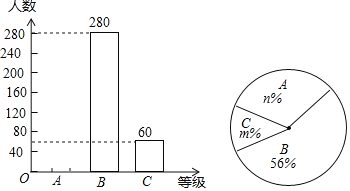
��1����ε������������Ϊ_____�ˣ�
��2����ȫ����ͳ��ͼ��
��3����������ͳ��ͼ�еȼ�C��Ӧ��Բ�ĽǵĶ�����
��4��������Լ������1000000�ˣ�������ݳ�������Ľ�������Ƹ��д�Լ�ж����˶������������ļ�ֵ�����ﵽ��A���dz��˽����ij̶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺��
(1)(-6)-(+5)+(-7)-(-4)
(2) (-8)![]() (-4)
(-4)![]()
(3)![]()
(4)![]()
(5)![]()
(6)![]() (
(![]() )
)![]()
(7)x+(5x+3y)-(3x-2y)
(8)(5a2+2a-1)-4(3-2a+a2)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������8�֣���ͼ����֪������y=��x2+bx+c��x�ύ�ڵ�A����1��0���͵�B��3��0������y�ύ�ڵ�C������BC�������ߵĶԳ����ڵ�E��D�������ߵĶ��㣮
��1����������ߵĽ���ʽ��
��2��ֱ��д����C�͵�D�����ꣻ
��3������P�ڵ�һ�����ڵ��������ϣ���S��ABP=4S��COE����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������о������һ�ֳ��÷�����������ѧϰ�������ʹ���ʽ����ظ�����㷨��ʱ������ ѧ���˾���֪ʶ����ѧ���˷���˼�����ڽ��з���ʱ����������Ӧ��ȷ����������Ҫ��������ʱ�Ȳ� �ظ���Ҳ����©��
���������ܣ���1���ڶԶ���ʽ![]() ��
��![]() ���з���ʱ�������������Ϊ����������Է�Ϊ�ļ��ࣿ����Դ�����Ϊ����������Է�Ϊ�ļ��ࣿ
���з���ʱ�������������Ϊ����������Է�Ϊ�ļ��ࣿ����Դ�����Ϊ����������Է�Ϊ�ļ��ࣿ
�������ã���2����֪ a, b �����������Ƚ� a b �� a b�Ĵ�С��
������˼������3����֪ a, b c ������������ ca b��ca b ���ж� b, c �ķ��ţ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ȳ���Ŀ���ʶ�����������ѧ�����Ķ���Ȥ��ijУΪ����ѧ�����Ķ�����������һ��ѧ��ϲ����ͼ�飬ѧУ��֯ѧ�����Ա�����ȡ����ѧ�������ʾ����飬������ѧ���������ʷ�ࡢ����ࡢС˵�ࡢ����������ѡ���Լ�ϲ����һ�࣬���ݵ�����������ͳ��ͼ��δ��ɣ��������ͼ����Ϣ������������⣺
��1���˴ι��������� ����ѧ����
��2��������ͳ��ͼ����������
��3��ͼ2����С˵�����������ε�Բ�Ľ�Ϊ�� ���ȣ�
��4������У����ѧ��2500�ˣ����Ƹ�Уϲ������������鼮��ѧ��������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com