
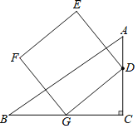
【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,点G为边BC的中点,点D从点C出发沿CA向点A运动,到点A停止,以GD为边作正方形DEFG,则点E运动的路程为_______.
【答案】3![]()
【解析】
建立下图所示的坐标系,过点E作EH⊥y轴,垂足为H,先证明△EDH≌△DGC,则DH=GC=2,DC=EH,设DC=t,则EH=t,点E的坐标为(-t,t+2),然后求得当t=0和t=3时点E的坐标,然后利用两点间的距离公式即可求解.
解:建立如图所示的坐标系,过点E作EH⊥y轴,垂足为H.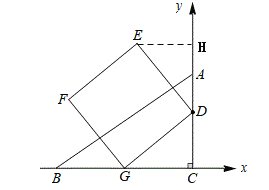
∵BC=4,点G为边BC的中点,
∴GC=2.
∵DEFG为正方形,
∴ED=DG,∠EDG=90°.
∴∠EDH+∠GDC=90°.
又∵∠EDH+∠HED=90°,
∴∠GDC=∠HED.
在△EDH和△DGC中,∠GDC=∠HED,∠EHD=∠DCG,ED=DG,
∴△EDH≌△DGC.
∴DH=GC=2,DC=EH.
设DC=t,则EH=t,
∴点E的坐标为(-t,t+2),
∴点E在直线y=-x+2.
由题意可知:0<t≤3,
当t=0时,y=2,E(0,2)
当t=3时,y=5,E(-3,5)
∴点E运动的路线长=![]() .
.
故答案为:3![]() .
.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图,在钟面上,点![]() 为钟面的圆心,以点
为钟面的圆心,以点![]() 为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
为顶点按要求画出符合下列要求的角(角的两边不经过钟面上的数字):
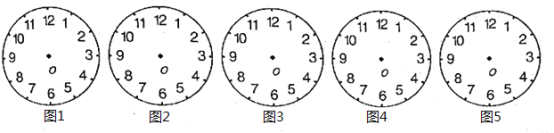
(1)在图1中画一个锐角,使锐角的内部含有2个数字,且数字之差的绝对值最大;
(2)在图2中画一个直角,使直角的内部含有3个数字,且数字之积等于数字之和;
(3)在图3中画一个钝角,使钝角的内部含有4个数字,且数字之和最小;
(4)在图4中画一个平角,使平角的内部与外部的数字之和相等;
(5)在图5中画两个直角,使这两个直角的内部含有的3个数字之和相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
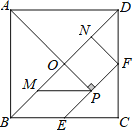
【题目】七巧板是一种古老的中国传统智力玩具.如图,在正方形纸板ABCD中,BD为对角线,E、F分别为BC、CD的中点,AP⊥EF分别交BD、EF于O、P两点,M、N分别为BO、DO的中点,连接MP、NF,沿图中实线剪开即可得到一副七巧板.若AB=1,则四边形BMPE的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
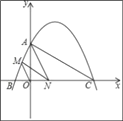
如图,二次函数y=﹣![]() x2+
x2+![]() x+4的图象与x轴交于点B,点C(点B在点C的左边),与y轴交于点A,连接AC,AB.
x+4的图象与x轴交于点B,点C(点B在点C的左边),与y轴交于点A,连接AC,AB.
(1)求证:AO2=BOCO;
(2)若点N在线段BC上运动(不与点B,C重合),过点N作MN∥AC,交AB于点M,求当△AMN的面积取得最大值时,直线AN的表达式.
(3)连接OM,在(2)的结论下,试判断OM与AN的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
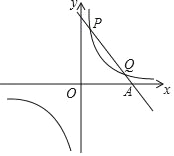
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内P(
的图象交于第一象限内P(![]() ,8),Q(4,m)两点.
,8),Q(4,m)两点.
(1)分别求出这两个函数的表达式;
(2)请直接写出不等式k1x+b<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3-1),B(-4,-3),C(-2,-3).
(1)画出将△ABC向上平移5个单位得到的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC关于点O成中心对称的图形△A2B2C2,并写出点B2的坐标;
(3)观察图形,△A1B1C1和△A2B2C2成中心对称吗?如果成中心对称,那么对称中心的坐标为_____;如果不成中心对称,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练,机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动,已知AD=6个单位长度,机器人的速度为1个单位长度/s且其移动至拐角处调整方向所需时间忽略不计.设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)图②中函数图象与纵轴的交点的纵坐标![]() 在图①中表示一条线段的长,请在图①中画出这条线段.
在图①中表示一条线段的长,请在图①中画出这条线段.
(2)求图②中a的值;
(3)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠3=∠E.试说明:∠A=∠EBC.(请按图填空,并补理由.)
证明:∵∠1=∠2 (已知),

∴________∥_______( ),
∴∠E=∠_______ ( ),
又∵∠E=∠3 (已知),
∴∠3=∠____________ ( 等量代换 ),
∴_________∥________ (内错角相等,两直线平行),
∴∠A=∠EBC ( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com