
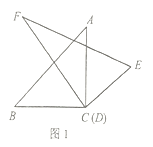
ЁОЬтФПЁПвЛИБШ§НЧАхЕФСНПщШ§НЧАхЕФШ§ИіНЧЖШЪ§ЗжБ№ЮЊ90ЁуЁЂ60ЁуЁЂ30ЁуКЭ90ЁуЁЂ45ЁуЁЂ45ЁуЃЌЮвУЧПЩвдгУШ§НЧАхЕФНЧЦДГівЛаЉЬиЪтЖШЪ§ЕФНЧЃЎ
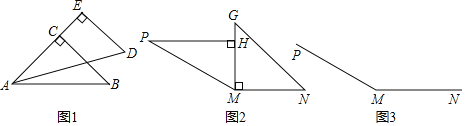
ЃЈ1ЃЉСНПщШ§НЧАхАДШчЭМ1ЫљЪОЦДНгЃЌдђЁЯBADЕФЖШЪ§ЪЧЁЁ ЁЁЁуЃЎ
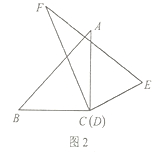
ЃЈ2ЃЉаЁУїгУСНПщШ§НЧАхАДЭМ2ЦДГіЕФЁЯPMNЕФЖШЪ§ЪЧЁЁ ЁЁЁуЃЎ
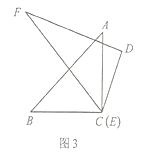
ЃЈ3ЃЉаЁУїЯыЛГіЭМ2ЦДГіЕФЁЯPMNЕФНЧЦНЗжЯпЃЌЧыФужЛгУвЛИБШ§НЧАхдкЭМ3жаАяаЁУїЭъГЩЛЭМЃЎЃЈВЛаДЛЗЈЃЌБЃСєЛЭМКлМЃЃЌБъГіБивЊЕФЖШЪ§ЃЉ
ЁОД№АИЁПЃЈ1ЃЉ15ЃЛЃЈ2ЃЉ150ЃЛЃЈ3ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉСНПщШ§НЧАхАДШчЭМ1ЫљЪОЦДНгЃЌЕУЁЯBADЕФЖШЪ§ЪЧ 45ЁуЉ30Ёу=15ЁуЃЎ
ЃЈ2ЃЉСНПщШ§НЧАхАДЭМ2ЦДГіЕФЁЯPMNЕФЖШЪ§ЪЧ90Ёу+60Ёу=150ЁуЃЎ
ЃЈ3ЃЉЛГіЭМ2ЦДГіЕФЁЯPMNЕФНЧЦНЗжЯпЃЌгУвЛИБШ§НЧАхЕФ45ЖШНЧМгЩЯ30ЖШНЧМДПЩдкЭМ3жаЭъГЩЛЭМЃЎ
НтЃКШчЭМЫљЪОЃК
ЃЈ1ЃЉШчЭМ1ЃЌЕУЃКЁЯBAD= ЁЯBACЁЯDAE=45ЁуЉ30Ёу=15ЁуЃЌ
ЙЪД№АИЮЊЃК15ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕУЃКЁЯPMN=ЁЯGMN+ЁЯPMH =90Ёу+60Ёу=150Ёу,
ЙЪД№АИЮЊЃК150ЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЁЯPMN=150Ёу,
ИљОнНЧЦНЗжЯпЕФЖЈвхЃЌЁЯPMNПЩЗжЮЊЖШЪ§ЖМЪЧ75ЁуЕФСНИіНЧЃЌ
дђгУвЛИБШ§НЧАхЕФ45ЖШНЧМгЩЯ30ЖШНЧМДПЩЕУГі75ЁуЃЌ
ЫљвдгУвЛИБШ§НЧАхЕФ45ЖШНЧМгЩЯ30ЖШНЧМДПЩдкЭМ3жаЭъГЩЛЭМЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1,дкRtЁїABCжаЃЌЁЯC=90,BC=6ЃЌAC=8.ЖЏЕуMДгЕуBПЊЪМбиБпBCЯђЕуCвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЖЏЕуNДгЕуCПЊЪМбиБпCAЯђЕуAвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌЕуMЁЂNЭЌЪБГіЗЂЃЌЧвЕБЦфжавЛЕуЕНДяЖЫЕуЪБЃЌСэвЛЕувВЫцжЎЭЃжЙдЫЖЏ.Й§ЕуMзїMDЁЮAC,НЛABгкЕуD,СЌНгMN.ЩшдЫЖЏЪБМфЮЊtУыЃЈtЁн0ЃЉ.
(1)ЕБtЮЊКЮжЕЪБЃЌЫФБпаЮADMNЮЊЦНааЫФБпаЮЃП
(2)ЪЧЗёДцдкtЕФжЕЃЌЪЙЫФБпаЮADMNЮЊСтаЮЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.ВЂЬНОПжЛИФБфЕуNЕФЫйЖШЃЈдШЫйдЫЖЏЃЉЃЌЪЙЫФБпаЮADMNдкФГвЛЪБПЬЮЊСтаЮЃЌЧѓЕуNЕФЫйЖШЃЛ
(3)ШчЭМ2ЃЌдкећИідЫЖЏЙ§ГЬжаЃЌЧѓГіЯпЖЮMNжаЕуPЫљОЙ§ЕФТЗОЖГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБНЧШ§НЧАх![]() КЭжБНЧШ§НЧАх
КЭжБНЧШ§НЧАх![]() ,
,![]() ,
,![]() ,
,
![]() .
.
(1)ШчЭМ1,НЋЖЅЕу![]() КЭЖЅЕу
КЭЖЅЕу![]() жиКЯ,БЃГжШ§НЧАх
жиКЯ,БЃГжШ§НЧАх![]() ВЛЖЏ,НЋШ§НЧАх
ВЛЖЏ,НЋШ§НЧАх![]() ШЦЕу
ШЦЕу![]() а§зЊ.ЕБ
а§зЊ.ЕБ![]() ЦНЗж
ЦНЗж![]() ЪБ,Чѓ
ЪБ,Чѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
(2)дк(1)ЕФЬѕМўЯТ,МЬаја§зЊШ§НЧАх![]() ,ВТЯы
,ВТЯы![]() гы
гы![]() гадѕбљЕФЪ§СПЙиЯЕ?ВЂРћгУЭМ2ЫљИјЕФЧщаЮЫЕУїРэгЩЃЛ
гадѕбљЕФЪ§СПЙиЯЕ?ВЂРћгУЭМ2ЫљИјЕФЧщаЮЫЕУїРэгЩЃЛ
(3)ШчЭМ3,НЋЖЅЕу![]() КЭЖЅЕу
КЭЖЅЕу![]() жиКЯ,БЃГжШ§НЧАх
жиКЯ,БЃГжШ§НЧАх![]() ВЛЖЏ,НЋШ§НЧАх
ВЛЖЏ,НЋШ§НЧАх![]() ШЦЕу
ШЦЕу![]() а§зЊ.ЕБ
а§зЊ.ЕБ![]() Тфдк
Тфдк![]() ФкВПЪБ,жБНгаДГі
ФкВПЪБ,жБНгаДГі![]() гы
гы![]() ЕФЪ§СПЙиЯЕ.
ЕФЪ§СПЙиЯЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЁїABCбиBCЗНЯђЦНвЦ2cmЕУЕНЁїDEFЃЌШєЁїABCЕФжмГЄЮЊ16cmЃЌtЫФоxаЮABFDЕФжмГЄЮЊ( )

A. 16cmB. 18cmC. 20cmD. 22cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМђЕЅЖрУцЬхЪЧИїИіУцЖМЪЧЖрБпаЮзщГЩЕФМИКЮЬхЃЌЪЎАЫЪРМЭШ№ЪПЪ§бЇМвХЗРжЄУїСЫМђЕЅЖрУцЬхжаЖЅЕуЪ§ЃЈVЃЉЁЂУцЪ§ЃЈFЃЉКЭРтЪ§ЃЈEЃЉжЎМфДцдквЛИігаШЄЕФЙиЯЕЪНЃЌГЦЮЊХЗРЙЋЪНЃЎШчБэЪЧИљОнзѓБпЕФЖрУцЬхФЃаЭСаГіЕФВЛЭъећЕФБэЃК
ЖрУцЬх | ЖЅЕуЪ§ | УцЪ§ | РтЪ§ |
ЫФУцЬх | 4 | 4 | 6 |
ГЄЗНЬх | 8 | 6 | |
е§АЫУцЬх | 8 | 12 |
ЯждкгавЛИіЖрУцЬхЃЌЫќЕФУПвЛИіУцЖМЪЧШ§НЧаЮЃЌЫќЕФУцЪ§ЃЈFЃЉКЭРтЪ§ЃЈEЃЉЕФКЭЮЊ30ЃЌдђетИіЖрУцЬхЕФЖЅЕуЪ§VЃН_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌЕуEдкBCЕФбгГЄЯпЩЯЃЌЧвCEЃНBCЃЌAEЃНABЃЌAEЁЂDCЯрНЛгкЕуOЃЌСЌНгDEЃЎШєЁЯAODЃН120ЁуЃЌACЃН4ЃЌдђCDЕФДѓаЁЮЊЃЈЁЁЁЁЃЉ
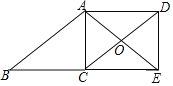
A.8B.4![]() C.8
C.8![]() D.6
D.6![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDКЭе§ЗНаЮCEFGжаЃЌЕуDдкCGЩЯЃЌвбжЊЃКBCЃН1ЃЌCEЃН7ЃЌHЪЧAFЕФжаЕуЃЌдђAFЃН_____ЃЌCHЃН_____ЃЎ
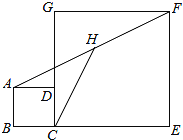
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊB(Ѓ1ЃЌ0)ЃЌвЛДЮКЏЪ§yЃНЃxЃЋ5ЕФЭМЯѓгыxжсЃЌyжсЗжБ№НЛгкЕуAЃЌCСНЕуЃЌЖўДЮКЏЪ§yЃНЃx2ЃЋbxЃЋcЕФЭМЯѓОЙ§ЕуAЃЌЕуB.
(1)ЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
(2)ЕуPЪЧИУЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуЃЌЧѓЁїAPCЕФУцЛ§ЃЛ
(3)ШчЙћЕуQдкЯпЖЮACЩЯЃЌЧвЁїABCгыЁїAOQЯрЫЦЃЌЧѓЕуQЕФзјБъЃЎ
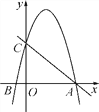
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇЮЊСЫдЄЗРСїааадИаУАЃЌЖдНЬЪвВЩгУвЉбЌЯћЖОЗЈНјааЯћЖОЃЌвбжЊвЉЮяШМЩеЪБЃЌЪвФкУПСЂЗНУзПеЦјжаЕФКЌвЉСП![]() гыЪБМф
гыЪБМф![]() ГЩе§БШР§ЃЎвЉЮяШМЩеКѓЃЌyгыxГЩЗДБШР§ЃЈШчЭМЫљЪОЃЉЃЌЯжВтЕУвЉЮя6minШМБЯЃЌДЫЪБЪвФкПеЦјжаУПСЂЗНУзЕФКЌвЉСПЮЊ4mgЃЌ
ГЩе§БШР§ЃЎвЉЮяШМЩеКѓЃЌyгыxГЩЗДБШР§ЃЈШчЭМЫљЪОЃЉЃЌЯжВтЕУвЉЮя6minШМБЯЃЌДЫЪБЪвФкПеЦјжаУПСЂЗНУзЕФКЌвЉСПЮЊ4mgЃЌ
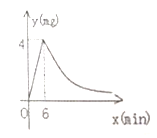
ЃЈ1ЃЉаДГівЉЮяШМЩеЧАКѓЃЌyгыxжЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉбаОПБэУїЃЌЕБПеЦјжаУПСЂЗНУзЕФКЌвЉСПЕЭгк1.6mgЪБбЇЩњЗНПЩНјНЬЪвЃЌФЧУДДгЯћЖОПЊЪМЃЌжСЩйашвЊОЙ§ЖрЩйЗжжгЃЌбЇЩњЗНФмЛиЕННЬЪвЃП
ЃЈ3ЃЉбаОПБэУїЃЌЕБПеЦјжаУПСЂЗНУзЕФКЌвЉСПВЛЕЭгк2mgЧвГжајЪБМфВЛЕЭгк9minЪБЃЌВХФмгааЇЩБУ№ПеЦјжаЕФВЁОњЃЌФЧУДДЫДЮЯћЖОЪЧЗёгааЇЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com