
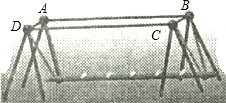
 如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.  举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
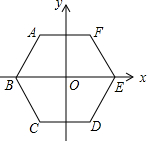 如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.
如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
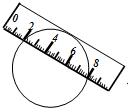 如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为6.5cm的圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则刻度尺的宽为2cm.
如图,两边平行的刻度尺在圆上移动,当刻度尺的一边与直径为6.5cm的圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则刻度尺的宽为2cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com