
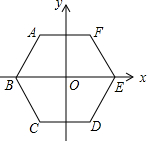
 如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.
如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$. 分析 连接OC,过点C作CH⊥x轴,垂足为H,易知CG=OH=1,在Rt△COH中,由正六边形的性质可得∠COH=60°,通过解直角三角形即可求得CH的长,也就得到了C点的坐标;同理可求得B、F的坐标,根据题意抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的B、C、F三个顶点,然后用待定系数法即可求得该抛物线的解析式.
解答 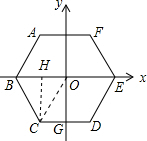 解:设CD与y轴交于点G,连接OC,过点C作CH⊥x轴,垂足为H;
解:设CD与y轴交于点G,连接OC,过点C作CH⊥x轴,垂足为H;
由已知CD=2,得CG=1,CH=$\sqrt{3}$,∠COH=60°(正六边形的性质),
∴C(-1,-$\sqrt{3}$);
同理F(1,$\sqrt{3}$),B(-2,0);
∵抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,
∴抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的B、C、F三个顶点,
∴$\left\{\begin{array}{l}{a-b+c=-\sqrt{3}}\\{a+b+c=\sqrt{3}}\\{4a-2b+c=0}\end{array}\right.$,
解此方程组,得$\left\{\begin{array}{l}{a=\frac{2\sqrt{3}}{3}}\\{b=\sqrt{3}}\\{c=-\frac{2\sqrt{3}}{3}}\end{array}\right.$;
因此所求二次函数解析式是y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.
故答案为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.
点评 此题主要考查了正六边形的性质及二次函数解析式的确定等知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| A(个) | B(个) | C(个) | |
| 方法1 | 2 | 0 | 0 |
| 方法2 | 0 | 6 | 0 |
| 方法3 | 0 | 2 | 2 |
| A(个) | B(个) | C(个) | |
| 甲模型(个) | 1 | 2 | 0 |
| 乙模型(个) | 0 | 1 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
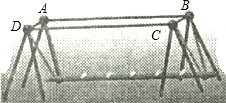 如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 ”可以得到美丽的“中国结”图案,左边四个图案是由“
”可以得到美丽的“中国结”图案,左边四个图案是由“ ”平移后得到的类似“中国结”的图案,按图中规律,第10个图案中,小菱形“
”平移后得到的类似“中国结”的图案,按图中规律,第10个图案中,小菱形“ ”的个数200.
”的个数200.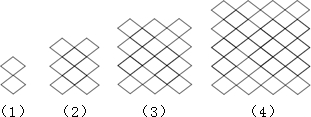
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
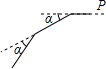 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )| A. | 30° | B. | 40° | C. | 80° | D. | 108° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
类型 编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com