
 ”可以得到美丽的“中国结”图案,左边四个图案是由“
”可以得到美丽的“中国结”图案,左边四个图案是由“ ”平移后得到的类似“中国结”的图案,按图中规律,第10个图案中,小菱形“
”平移后得到的类似“中国结”的图案,按图中规律,第10个图案中,小菱形“ ”的个数200.
”的个数200.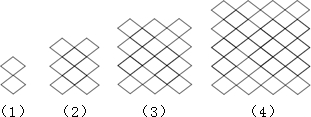
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
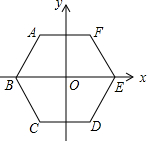 如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.
如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
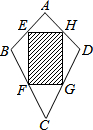 某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( )
某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( )| A. | 15匹 | B. | 20匹 | C. | 60匹 | D. | 30匹 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com