
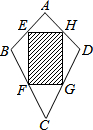
 某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( )
某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( )| A. | 15匹 | B. | 20匹 | C. | 60匹 | D. | 30匹 |
分析 连接AC、BD,根据三角形中位线定理证明△BEF∽△BAC,且相似比为1:2,则面积比为1:4,同理证明阴影部分面积等于如图所示的风筝面积的一半,得到答案.
解答 解: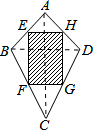 连接AC、BD,
连接AC、BD,
∵点E、F分别是AB、BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
∴△BEF∽△BAC,
∴S△BEF=$\frac{1}{4}$S△BAC,
同理,S△DHG=$\frac{1}{4}$S△DAC,
则S△BEF+S△DHG=$\frac{1}{4}$S△BAC+$\frac{1}{4}$S△DAC=$\frac{1}{4}$S四边形ABCD,
同理S△AEH+S△CFG=$\frac{1}{4}$S四边形ABCD,
∴阴影部分面积等于如图所示的风筝面积的一半,
即阴影部分面积与其余部分面积相等,
生产这批风筝需要甲布料30匹,那么需要乙布料也是30匹,
故选:D.
点评 本题考查的是中点四边形的知识,掌握三角形中位线定理和相似三角形的面积比等于相似比的平方是解题的关键.


科目:初中数学 来源: 题型:填空题
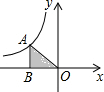 如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于点B.若S△AOB=4,则这个反比例函数的解析式为y=-$\frac{8}{x}$.
如图,点A在反比例函数y=$\frac{k}{x}$的图象上,AB垂直x轴于点B.若S△AOB=4,则这个反比例函数的解析式为y=-$\frac{8}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A(个) | B(个) | C(个) | |
| 方法1 | 2 | 0 | 0 |
| 方法2 | 0 | 6 | 0 |
| 方法3 | 0 | 2 | 2 |
| A(个) | B(个) | C(个) | |
| 甲模型(个) | 1 | 2 | 0 |
| 乙模型(个) | 0 | 1 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 ”可以得到美丽的“中国结”图案,左边四个图案是由“
”可以得到美丽的“中国结”图案,左边四个图案是由“ ”平移后得到的类似“中国结”的图案,按图中规律,第10个图案中,小菱形“
”平移后得到的类似“中国结”的图案,按图中规律,第10个图案中,小菱形“ ”的个数200.
”的个数200.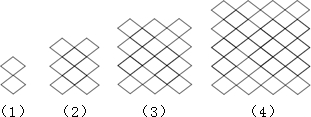
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
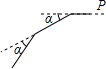 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )| A. | 30° | B. | 40° | C. | 80° | D. | 108° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
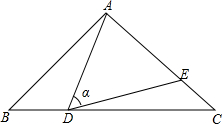 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
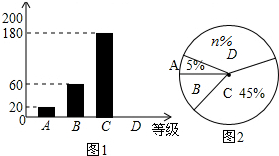 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:| 对提议的了解程度 | 百分比 |
| A、非常了解 | 5% |
| B、比较了解 | m |
| C、基本了解 | 45% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
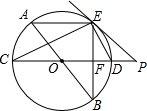 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com