
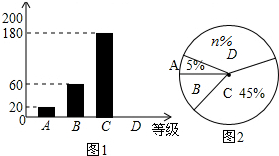
 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:| 对提议的了解程度 | 百分比 |
| A、非常了解 | 5% |
| B、比较了解 | m |
| C、基本了解 | 45% |
分析 (1)根据“基本了解”的人数以及所占比例,可求得总人数;在根据频数、百分比之间的关系,可得m,n的值;
(2)根据在扇形统计图中,每部分占总体的百分比等于该部分所对应的扇形圆心的度数与360°的比可得出统计图中D部分扇形所对应的圆心角;
(3)根据D等级的人数为:400×35%=140;可得(3)的答案;
(4)用树状图列举出所有可能,进而得出答案.
解答 解:(1)∵利用条形图和扇形图可得出:本次参与调查的学生共有:180÷45%=400(人);
∴m=$\frac{60}{400}$×100%=15%,n%=1-5%-15%-45%=35%;
∴n=35;
故答案为:400,15%,35;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是:360°×35%=126°;
故答案为:126;
(3)D等级的人数为:400×35%=140(人);
如图所示: ;
;
(4)列树状图得: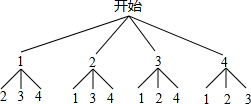
∵从树状图可以看出所有可能的结果有12种,数字之和为奇数的有8种,
∴小明参加的概率为:P=$\frac{8}{12}$=$\frac{2}{3}$,小刚参加的概率为:P=$\frac{4}{12}$=$\frac{1}{3}$,
故游戏规则不公平.
点评 此题主要考查了游戏公平性,涉及扇形统计图的意义与特点,即可以比较清楚地反映出部分与部分、部分与整体之间的数量关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
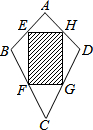 某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( )
某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( )| A. | 15匹 | B. | 20匹 | C. | 60匹 | D. | 30匹 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
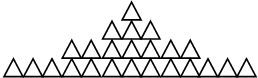 如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要21个三角形…摆到第n层需要n2-n+1个三角形.
如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要21个三角形…摆到第n层需要n2-n+1个三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com